“割圓術”是劉徽最突出的數學成就之一，他在《九章算術注》中提出割圓術，并作為計算圓的周長、面積以及圓周率的基礎劉徽把圓內接正多邊形的面積直算到了正3072邊形，并由此而求得了圓周率為3.1415和3.1416這兩個近似數值，這個結果是當時世界上圓周率計算的最精確數據．如圖，當分割到圓內接正六邊形時，某同學利用計算機隨機模擬法向圓內隨機投擲點，計算得出該點落在正六邊形內的頻率為0.8269，那么通過該實驗計算出來的圓周率近似值為（ ）（參考數據30.826=2.0946）
3
0
.
826
【考點】幾何概型．
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/29 8:0:9組卷：219引用：23難度：0.7
相似題
-
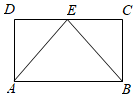1．如圖，矩形ABCD中，點E為邊CD的中點，若在矩形ABCD內部隨機取一個點Q，則點Q取自△ABE內部的概率等于．發布：2025/1/13 8:0:2組卷：30引用：12難度：0.7 -
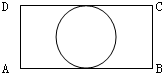2．如圖所示，在矩形ABCD中，AB=4cm,BC=2cm,在圖形上隨機撒一粒黃豆，則黃豆落到圓上的概率是．發布：2025/1/13 8:0:2組卷：9引用：2難度：0.7 -
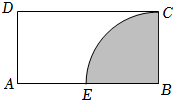3．如圖，矩形ABCD，AB=2，BC=1，陰影部分為B為圓心，BC為半徑的圓與矩形的重合部分，現在向矩形內隨機投擲一點，則該點落在陰影部分以外的概率為（ ）發布：2024/12/29 15:30:4組卷：1引用：1難度：0.7