定義：如果四邊形的一條對角線的中點到另外兩個頂點的距離都等于這條對角線長的一半，那么我們稱這樣的四邊形為“等距四邊形”．
（1）在下列圖形中：①平行四邊形、②矩形、③菱形，一定是“等距四邊形”的是 ②②；（填序號）
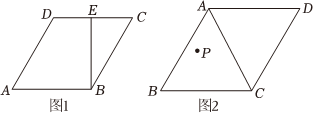
（2）如圖1，在菱形ABCD中，AB=4，∠A=60°，BE⊥CD于點E，點F是菱形ABCD邊上的一點，順次連接B、E、D、F，若四邊形BEDF為“等距四邊形”，求線段EF的長；
（3）如圖2，在?ABCD中，AD=CD=4，AB=AC，點P是△ABC內一點，在AB、BC、CA上是否分別存在點，使得這些點與點P的連線將△ABC恰好分割成三個“等距四邊形”，若存在，求這三個“等距四邊形”的周長和，若不存在，請說明理由．
【考點】四邊形綜合題．
【答案】②
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/25 16:0:10組卷：44引用：1難度：0.1
相似題
-
1．（1）如圖1，在四邊形ABCD中，DA=DC，∠A=∠C=90°，E、F分別是邊AB、BC上的點，且∠EDF=
∠ADC，請直接寫出圖中線段AE、EF、FC之間的數量關系 ．12
（2）如圖2，在四邊形ABCD中，DA=DC，∠A+∠C=180°，E、F分別是邊AB、BC上的點，且∠EDF=∠ADC，上述結論是否仍然成立，并說明理由．12
（3）如圖3，在四邊形ABCD中，DA=DC，∠A+∠BCD=180°，E、F分別是邊AB、BC延長線上的點，且∠EDF=∠ADC，（1）中的結論是否仍然成立？若成立，請證明；若不成立，線段AE、EF、FC之間又有怎樣的數量關系，請直接寫出你的猜想，并說明理由．12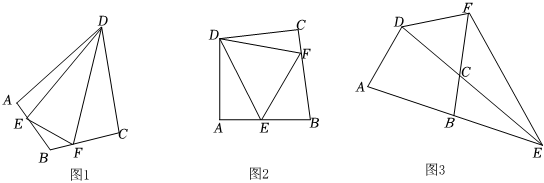
發布：2025/6/9 2:30:1組卷：165引用：1難度：0.2 -
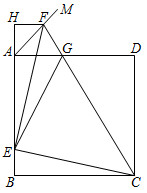2．如圖，正方形ABCD的邊長為4，點E在邊AB上，BE=1，∠DAM=45°，點F在射線AM上，且AF=，過點F作AD的平行線交BA的延長線于點H，CF與AD相交于點G，連接EC、EG，EF．下列結論：①∠EFG=45°；②△AEG的周長為8；③△CEG∽△AFG；④△CEG的面積為6.8．其中正確的個數是（ ）2發布：2025/6/9 3:0:1組卷：680引用：3難度：0.2 -
3．下面是小明復習全等三角形時遇到的一個問題并引發的思考，請幫助小明完成以下學習任務．
如圖，OC平分∠AOB，點P在OC上，M、N分別是OA、OB上的點，OM=ON，求證：PM=PN．
小明的思考：要證明PM=PN，只需證明△POM≌△PON即可．
證法：如圖1，∵OC平分∠AOB，∴∠AOC=∠BOC，
又∵OP=OP，OM=ON，∴△MOP≌△NOP，
∴PM=PN；
請仔細閱讀并完成以下任務：
（1）小明得出△MOP≌△NOP的依據是 （填序號）．
①SSS，②SAS，③AAS，④ASA，⑤HL．
（2）如圖②，在四邊形ABCD中，AB=AD+BC，∠DAB的平分線和∠ABC的平分線交于CD邊上點P，求證：PC=PD．
（3）在（2）的條件下，如圖③，若AB=10，tan∠PAB=，當△PBC有一個內角是45°時，△PAD的面積是 ．12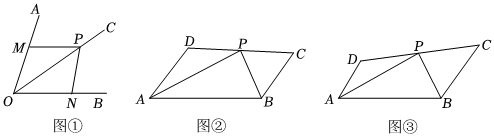
發布：2025/6/9 3:30:1組卷：114引用：3難度：0.3