對于平面直角坐標系xOy中的圖形M和點P，給出如下定義：將圖形M繞點P順時針旋轉90°得到圖形N，圖形N稱為圖形M關于點P的“垂直圖形”．例如，圖1中點D為點C關于點P的“垂直圖形”
（1）點A關于原點O的“垂直圖形”為點B．
①若點A的坐標為（0，2），則點B的坐標為 （2，0）（2，0）；
②若點B的坐標為（2，1），則點A的坐標為 （-1，2）（-1，2）；
（2）E（-3，3），F（-2，3），G（a,0）．線段EF關于點G的“垂直圖形”記為E′F′，點E的對應點為E′，點F的對應點為F′．
①求點E′的坐標（用含a的式子表示）；
②若⊙O的半徑為2，E′F′上任意一點都在⊙O內部或圓上，直接寫出滿足條件的EE′的長度的最大值．
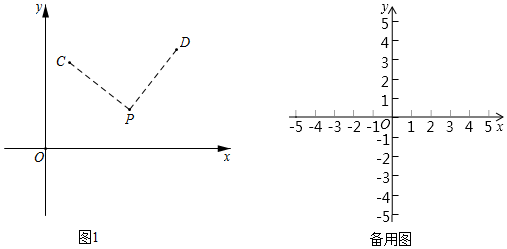
【考點】幾何變換綜合題．
【答案】（2，0）；（-1，2）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/27 16:0:2組卷：867引用：5難度：0.1
相似題
-
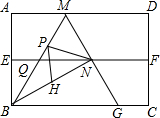1．如圖，四邊形ABCD是矩形紙片，AB=2．對折矩形紙片ABCD，使AD與BC重合，折痕為EF；展平后再過點B折疊矩形紙片，使點A落在EF上的點N，折痕BM與EF相交于點Q；再次展平，連接BN，MN，延長MN交BC于點G．有如下結論：
①∠ABN=60°；②AM=1；③QN=；④△BMG是等邊三角形；⑤P為線段BM上一動點，H是BN的中點，則PN+PH的最小值是33．3
其中正確結論的序號是．發布：2025/5/23 1:30:2組卷：3126引用：15難度：0.5 -
2．如圖1，四邊形ABCD中，∠BCD=90°，AC=AD，AF⊥CD于點F，交BD于點E，∠ABD=2∠BDC．
（1）判斷線段AE與BC的關系，并說明理由；
（2）若∠BDC=30°，求∠ACD的度數；
（3）如圖2，在（2）的條件下，線段BD與AC交于點O，點G是△BCE內一點，∠CGE=90°，GE=3，將△CGE繞著點C逆時針旋轉60°得△CMH，E點對應點為M，G點的對應點為H，且點O，G，H在一條直線上直接寫出OG+OH的值．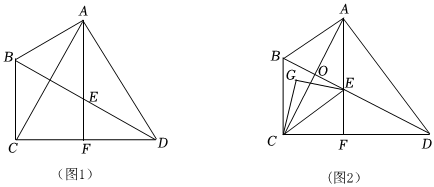
發布：2025/5/22 19:0:1組卷：523引用：1難度：0.2 -
3．在△ABC中，AB=AC，∠BAC=α，點P為線段CA延長線上一動點，連接PB，將線段PB繞點P逆時針旋轉，旋轉角為α，得到線段PD，連接DB，DC．
（1）如圖1，當α=60°時，
①求證：PA=DC；
②求∠DCP的度數；
（2）如圖2，當α=120°時，請直接寫出PA和DC的數量關系．
（3）當α=120°時，若AB=6，BP=，請直接寫出點D到CP的距離為．31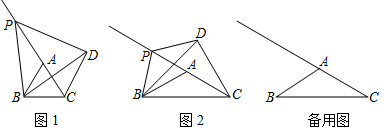
發布：2025/5/23 4:0:1組卷：4734引用：13難度：0.1