在△ABC中，∠A=90°，AB=8cm,AC=6cm,點M，點N同時從點A出發，點M
沿邊AB以4cm/s的速度向點B運動，點N從點A出發，沿邊AC以3cm/s的速度向點C運動（點M不與A，B重合，點N不與A，C重合），設運動時間為xs.
（1）求證：△AMN∽△ABC；
（2）當x為何值時，以MN為直徑的⊙O與直線BC相切？
（3）把△AMN 沿直線MN折疊得到△MNP，若△MNP 與梯形BCNM重疊部分的面積為y,試求y關于x的函數表達式，并求x為何值時，y的值最大，最大值是多少？
【考點】圓的綜合題．
【答案】（1）見解答；
（2）當x=時，⊙O與直線BC相切；
（3）當時，y值最大，最大值是8．
（2）當x=
48
49
（3）當
x
=
4
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/21 8:0:9組卷：49引用：1難度：0.2
相似題
-
1．約定：若三角形一邊上的中線將三角形分得的兩個小三角形中有一個三角形與原三角形相似，我們則稱原三角形為關于該邊的“優美三角形”．例如：如圖1，在△ABC中，AD為邊BC上的中線，△ABD與△ABC相似，那么稱△ABC為關于邊BC的“優美三角形”．
（1）如圖2，在△ABC中，BC=AB，求證：△ABC為關于邊BC的“優美三角形”；2
（2）如圖3，已知△ABC為關于邊BC的“優美三角形”，點D是△ABC邊BC的中點，以BD為直徑的⊙O恰好經過點A．
①求證：直線CA與⊙O相切；
②若⊙O的直徑為2，求線段AB的長；6
（3）已知三角形ABC為關于邊BC的“優美三角形”，BC=4，∠B=30°，求△ABC的面積．
發布：2025/5/26 6:0:1組卷：572引用：1難度：0.3 -
2．如圖，在平面直角坐標系中，直線分別交x軸，y軸于點A，B，以AB為直徑構造圓，點C在y=-34x+6運動，點D在?BO上，CD交OA于點P，且?CA．?CD=?OA
（1）求CD的長．
（2）求證：OP=PD．
（3）CE∥OA，交圓于另一點E，連結DE．若△CDE為等腰三角形，求所有滿足條件的點P的坐標．發布：2025/5/26 6:0:1組卷：354引用：1難度：0.2 -
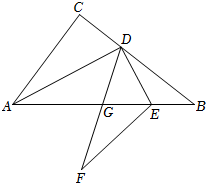3．如圖，在△ABC中，∠C=90°，AD平分∠BAC，AD⊥DE，DF平分∠ADE交AB于點G，∠ADF=∠AEF．
（1）求證：△EDF∽△GEF；
（2）求證：BD是以AE為直徑的圓的切線；
（3）若tan∠AED=2，EF=2，求線段DF的長．10發布：2025/5/26 5:30:2組卷：104引用：3難度：0.4
相關試卷