【閱讀材料】說(shuō)明代數(shù)式x2+1+（x-3）2+4的幾何意義，并求它的最小值．
解：x2+1+（x-3）2+4=（x-0）2+（0-1）2+（x-3）2+（0-2）2，如圖1，建立平面直角坐標(biāo)系，點(diǎn)P（x,0）是x軸上一點(diǎn)，則（x-0）2+（0-1）2可以看成點(diǎn)P與點(diǎn)A（0，1）的距離，（x-3）2+（0-2）2可以看成點(diǎn)P與點(diǎn)B（3，2）的距離，所以原代數(shù)式的值可以看成線段PA與PB長(zhǎng)度之和，它的最小值就是求PA+PB的最小值．
設(shè)點(diǎn)A關(guān)于x軸的對(duì)稱點(diǎn)為A′，則PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而點(diǎn)A′、B間的直線段距離最短，所以PA′+PB的最小值為線段A′B的長(zhǎng)度．為此，構(gòu)造直角三角形A′CB，因?yàn)锳′C=3，CB=3，所以A′B=32，即原式的最小值為32．
根據(jù)以上閱讀材料，解答下列問(wèn)題：
【基礎(chǔ)訓(xùn)練】（1）代數(shù)式（x-1）2+1+（x-3）+16的值可以看成平面直角坐標(biāo)系中點(diǎn)P（x,0）與點(diǎn)A（1，1）、點(diǎn)B （3，4）或（3，-4）（3，4）或（3，-4）的距離之和；（填寫(xiě)點(diǎn)B的坐標(biāo)）
【能力提升】（2）求代數(shù)式x2+49+x2-12x+37的最小值為 （0，7）（0，7）；
【拓展升華】（3）如圖2，在等腰直角△ABC中，∠BAC=90°，點(diǎn)M，N分別為BC，AC上的動(dòng)點(diǎn)，且AN=CM，AB=2．當(dāng)AM+BN的值最小時(shí)，求CM的長(zhǎng)．
x
2
+
1
+
（
x
-
3
）
2
+
4
x
2
+
1
+
（
x
-
3
）
2
+
4
=
（
x
-
0
）
2
+
（
0
-
1
）
2
+
（
x
-
3
）
2
+
（
0
-
2
）
2
（
x
-
0
）
2
+
（
0
-
1
）
2
（
x
-
3
）
2
+
（
0
-
2
）
2
A
′
B
=
3
2
3
2
（
x
-
1
）
2
+
1
+
（
x
-
3
）
+
16
x
2
+
49
+
x
2
-
12
x
+
37
AN
=
CM
，
AB
=
2
【考點(diǎn)】三角形綜合題．
【答案】（3，4）或（3，-4）；（0，7）
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：370引用：2難度：0.1
相似題
-
1．在平面直角坐標(biāo)系中，點(diǎn)A、B、C的坐標(biāo)分別為（m,0），（2，-4），（n,0），且m,n滿足方程（m-2）xn-4+
=0為二元一次方程．ym2-3
（1）求A、C的坐標(biāo)；
（2）若點(diǎn)D為y軸正半軸上的一個(gè)動(dòng)點(diǎn)．
①如圖1，已知∠DAO=∠ACB，∠ADO與∠ACB的角平分線交于點(diǎn)P，求∠P的度數(shù)；
②如圖2，連接BD，交x軸于點(diǎn)E．若S△ADE≤S△BCE成立．設(shè)動(dòng)點(diǎn)D坐標(biāo)為（0，a），求a的取值范圍．
發(fā)布：2025/6/8 0:30:1組卷：83引用：1難度：0.1 -
2．在平面直角坐標(biāo)系中，A（a,0），C（b,2），且滿足（a+b）2+|a-b+4|=0，過(guò)C作CB⊥x軸于B．
（1）如圖1，求△ABC的面積．
（2）如圖2，若過(guò)B作BD∥AC交y軸于D，在△ABC內(nèi)有一點(diǎn)E，連接AE、DE，若∠CAE+∠BDE=∠EAO+∠EDO，求∠AED的度數(shù)．
（3）如圖3，在（2）的條件下，DE與x軸交于點(diǎn)M，AC與y軸交于點(diǎn)F，作△AME的角平分線MP，在PE上有一點(diǎn)Q，連接QM，∠EAM+2∠PMQ=45°，當(dāng)AE=mAM，F(xiàn)O=2QM時(shí)，求點(diǎn)E的縱坐標(biāo)（用含m的代數(shù)式表示）．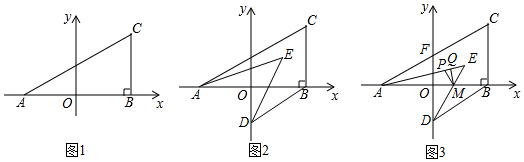
發(fā)布：2025/6/7 23:0:2組卷：189引用：2難度：0.2 -
3．如圖，在平面直角坐標(biāo)系xOy中，已知A（a,0），B（b,m），且滿足（a-6）2+
=0，m是36的算術(shù)平方根，將線段OA平移至CB，點(diǎn)D在x軸正半軸上（不與點(diǎn)A重合），連接OC，AB，CD，BD．b-8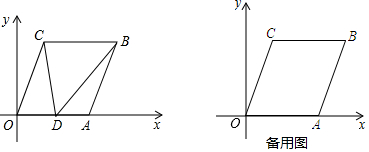
（1）直接寫(xiě)出點(diǎn)A、B、C的坐標(biāo)；
（2）當(dāng)△ODC的面積是△ABD的面積的3倍時(shí)，求點(diǎn)D的坐標(biāo)；
（3）已知OC∥AB，設(shè)∠OCD=α，∠DBA=∠β，∠BDC=θ，判斷α、β、θ之間的數(shù)量關(guān)系，并說(shuō)明理由．發(fā)布：2025/6/7 21:30:1組卷：284引用：4難度：0.4