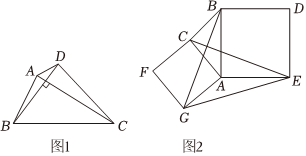
小明學習了平行四邊形這一章后，對特殊四邊形的探究產生了興趣，發現另外一類特殊四邊形，如圖1，我們把兩條對角線互相垂直的四邊形叫做垂美四邊形．
（1）概念理解：在平行四邊形、矩形、菱形、正方形中，一定是垂美四邊形的是 菱形、正方形菱形、正方形
（2）性質探究：通過探究，直接寫出垂美四邊形ABCD的面積S與兩對角線AC，BD之間的數量關系：12AC?BD12AC?BD．
（3）問題解決：如圖2，分別以Rt△ACB的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE，連接CG，BE，GE，已知AC=4，AB=5．
①求證：四邊形BCGE為垂美四邊形；
②求出四邊形BCGE的面積．
1
2
1
2
【考點】四邊形綜合題．
【答案】菱形、正方形；AC?BD
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/3 8:0:9組卷：561引用：6難度：0.3
相似題
-
1．如圖1和2，四邊形ABCD中，已知AB=AD，∠BAD=90°，點E、F分別在BC、CD上，∠EAF=45°．
（1）如圖1，若∠B、∠ADC都是直角，把△ABE繞點A逆時針旋轉90°至△ADG，使AB與AD重合，則能證得EF=BE+DF，請寫出推理過程；
（2）如圖2，若∠B、∠D都不是直角，則當∠B與∠D滿足數量關系時，仍有EF=BE+DF；
（3）拓展：如圖3，在△ABC中，∠BAC=90°，AB=AC=，點D、E均在邊BC上，且∠DAE=45°．若BD=3，求DE的長．62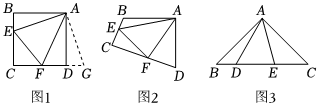
發布：2025/5/21 11:30:1組卷：107引用：1難度：0.1 -
2．在梯形ABCD中，AD∥BC，AD=4，∠ABC=90°，BD=BC，過點C作對角線BD的垂線，垂足為E，交射線BA于點F．
（1）如圖，當點F在邊AB上時，求證：△ABD≌△ECB；
（2）如圖，如果F是AB的中點，求FE：EC的值；
（3）聯結DF，如果△BFD是等腰三角形，求BC的長．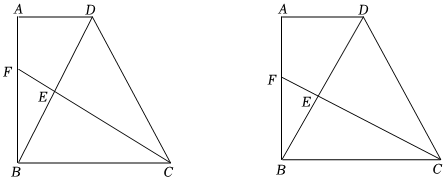
發布：2025/5/21 10:30:2組卷：450引用：1難度：0.2 -
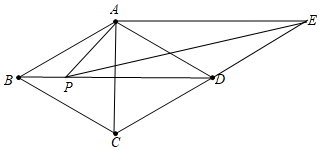3．如圖，在菱形ABCD中，∠ABC=60°，AB=2．過點A作對角線BD的平行線與邊CD的延長線相交于點E．P為邊BD上的一個動點（不與端點B，D重合），連接PA，PE，AC．
（1）求證：四邊形ABDE是平行四邊形；
（2）求四邊形ABDE的周長和面積；
（3）記△ABP的周長和面積分別為C1和S1，△PDE的周長和面積分別為C2和S2，在點P的運動過程中，試探究下列兩個式子的值或范圍：①C1+C2，②S1+S2，如果是定值的，請直接寫出這個定值；如果不是定值的，請直接寫出它的取值范圍．發布：2025/1/28 8:0:2組卷：577引用：1難度：0.2