四邊形ABCD為正方形,點E為線段AC上一點,連接DE,過點E作EF⊥DE,交射線BC于點F,以DE、EF為鄰邊作矩形DEFG,連接CG.
(1)如圖1,求證:矩形DEFG是正方形;
(2)若AB=2,CE=√2,求CG的長度;
(3)當線段DE與正方形ABCD的某條邊的夾角是30°時,直接寫出∠EFC的度數.

√
2
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/19 8:0:9組卷:10610引用:33難度:0.3
相似題
-
1.在正方形ABCD的邊AB、BC、CD、DA上分別任意取點E、F、G、H.這樣得到的四邊形EFGH中,是正方形的有( )
A.1個 B.2個 C.4個 D.無窮多個 發布:2025/5/28 17:0:2組卷:1143引用:6難度:0.9 -
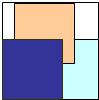 2.如圖,在一個大正方形內,放入三個面積相等的小正方形紙片,這三張紙片蓋住的總面積是24平方厘米,且未蓋住的面積比小正方形面積的四分之一還少3平方厘米,則大正方形的面積是(單位:平方厘米)( )
2.如圖,在一個大正方形內,放入三個面積相等的小正方形紙片,這三張紙片蓋住的總面積是24平方厘米,且未蓋住的面積比小正方形面積的四分之一還少3平方厘米,則大正方形的面積是(單位:平方厘米)( )A.40 B.25 C.26 D.36 發布:2025/5/27 10:30:1組卷:1079引用:3難度:0.7 -
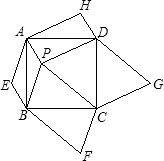 3.如圖,P為正方形ABCD內的一點,畫?PAHD,?PBEA,?PCFB,?PDGC,請證明:以E,F,G,H為頂點的四邊形是正方形.發布:2025/5/27 12:30:2組卷:1049引用:1難度:0.1
3.如圖,P為正方形ABCD內的一點,畫?PAHD,?PBEA,?PCFB,?PDGC,請證明:以E,F,G,H為頂點的四邊形是正方形.發布:2025/5/27 12:30:2組卷:1049引用:1難度:0.1


