如圖，ABCD是邊長為2a的正方形磁性約束裝置，內部存在垂直紙面方向的勻強磁場，AB、CD中點O、O′處各有一窄縫。平行金屬板M、N和BC邊平行，長度為2a、兩板間距離為a,其中M板緊靠BC邊且中點處的窄縫與BC邊的窄縫對齊，在金屬板M、N上加電壓UMN時，兩板間產生的電場可看成勻強電場。粒子源P不斷向外釋放電量為q＞0、質量為m的粒子，速度大小在0＜v≤v0之間，各個方向上的粒子數均勻分布。測量發現每秒有N個粒子從O′點射出，其中速度大小為v0的粒子恰能垂直BC邊從窄縫射出。不考慮粒子所受重力和粒子間相關作用力，不考慮電、磁場邊界效應，粒子撞到裝置邊界或極板后馬上被吸收并立即通過接地線被導走。求：
（1）ABCD內磁場的磁感應大小和方向；
（2）打到BC邊的粒子中，在磁場中運動的最短時間；
（3）當UMN=0時，N板上有粒子打到的區域的長度；
（4）請定性畫出每秒打到N板上的粒子數n與電壓UMN的關系圖線（需標注特征點）。
【答案】（1）ABCD內磁場的磁感應大小為，垂直紙面向外；
（2）打到BC邊的粒子中，在磁場中運動的最短時間為；
（3）當UMN=0時，N板上有粒子打到的區域的長度為a；
（4）見解析。
m
v
0
qa
（2）打到BC邊的粒子中，在磁場中運動的最短時間為
πa
3
v
0
（3）當UMN=0時，N板上有粒子打到的區域的長度為a；
（4）見解析。
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/23 12:26:7組卷：50引用：2難度：0.5
相似題
-
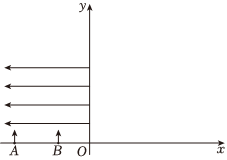1．在如圖所示的平面直角坐標系中，第二象限內存在水平向左的勻強電場，在x軸上有兩個粒子源A、B，沿y軸正向以相同速度同時發射質量相同、電荷量相同的帶負電的粒子，粒子源A、B的坐標分別為xA=-9L、xB=-4L。通過電場后A、B兩處發射的粒子分別從y軸上的C、D兩點（圖中未畫出）進入第一象限。不計粒子重力及粒子間的相互作用。
（1）設C、D兩點坐標分別為（0，yC）、（0，yD），求yC、yD的比值；
（2）若第一象限內未加任何場，兩處粒子將在第一象限內某點相遇，求相遇點的橫坐標；
（3）若第一象限內y＞yC區域，加上垂直于坐標平面方向向里的勻強磁場（圖中未畫出），兩處粒子最終將從磁場飛出，求兩處粒子飛出位置間的距離。發布：2024/12/29 20:30:1組卷：25引用：3難度：0.4 -
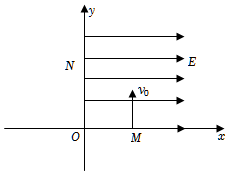2．如圖，在xOy坐標系中的第一象限內存在沿x軸正方向的勻強電場，第二象限內存在方向垂直紙面向外磁感應強度B=的勻強磁場，磁場范圍可調節（圖中未畫出）。一粒子源固定在x軸上M（L，0）點，沿y軸正方向釋放出速度大小均為v0的電子，電子經電場后從y軸上的N點進入第二象限。已知電子的質量為m,電荷量的絕對值為e,ON的距離3mv02eL，不考慮電子的重力和電子間的相互作用，求：233L
（1）第一象限內所加電場的電場強度；
（2）若磁場充滿第二象限，電子將從x軸上某點離開第二象限，求該點的坐標；
（3）若磁場是一個圓形有界磁場，要使電子經磁場偏轉后通過x軸時，與y軸負方向的夾角為30°，求圓形磁場區域的最小面積。發布：2024/12/29 23:30:1組卷：255引用：5難度：0.3 -
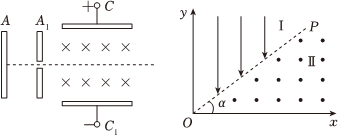3．在“質子療法”中，質子先被加速到具有較高的能量，然后被引向轟擊腫瘤，殺死細胞。如圖所示，質量為m、電荷量為q的質子從極板A處由靜止加速，通過極板A1中間的小孔后進入速度選擇器，并沿直線運動。速度選擇器中的勻強磁場垂直紙面向里，磁感應強度大小為B=0.01T，極板CC1間的電場強度大小為E=1×105N/C。坐標系xOy中yOP區域充滿沿y軸負方向的勻強電場Ⅰ，xOP區域充滿垂直紙面向外的勻強磁場Ⅱ，OP與x軸夾角a=30°。勻強磁場Ⅱ的磁感應強度大小B1，且1T≤B1≤1.5T。質子從（0，d）點進入電場Ⅰ，并垂直OP進入磁場Ⅱ。取質子比荷為，d=0.5m。求：qm=1×108C/kg
（l）極板AA1間的加速電壓U；
（2）勻強電場Ⅰ的電場強度E1；
（3）質子能到達x軸上的區間的長度L（結果用根號表示）。發布：2024/12/29 20:30:1組卷：120引用：3難度：0.6