當前位置：
試題詳情
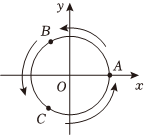如圖，直角坐標系中，圓的方程為x2+y2=1，A（1，0），B（-12，32），C（-12，-32）為圓上三個定點，某同學從A點開始，用擲骰子的方法移動棋子．規定：①每擲一次骰子，把一枚棋子從一個定點沿圓弧移動到相鄰下一個定點；②棋子移動的方向由擲骰子決定，若擲出骰子的點數為偶數，則按圖中箭頭方向移動；若擲出骰子的點數為奇數，則按圖中箭頭相反的方向移動．
設擲骰子n次時，棋子移動到A，B，C處的概率分別為Pn（A），Pn（B），Pn（C）．例如：擲骰子一次時，棋子移動到A，B，C處的概率分別為P1（A）=0，P1（B）=12，P1（C）=12．
（1）分別擲骰子二次，三次時，求棋子分別移動到A，B，C處的概率；
（2）擲骰子n次時，若以x軸非負半軸為始邊，以射線OA，OB，OC為終邊的角的余弦值記為隨機變量Xn，求X4的分布列和數學期望；
（3）記Pn（A）=an，Pn（B）=bn，Pn（C）=cn，其中an+bn+cn=1．證明：數列{bn-13}是等比數列，并求a2000．
1
2
3
2
1
2
3
2
1
2
1
2
1
3
【考點】離散型隨機變量的均值（數學期望）．
【答案】（1），，；，，．
（2）X4的分布列為：
E（X4）=．
（3）證明過程見解答，．
1
2
1
4
1
4
1
4
3
8
3
8
（2）X4的分布列為：
| X4 | 1 | - 1 2 |
| P | 3 8 |
5 8 |
1
16
（3）證明過程見解答，
1
3
[
1
+
（
1
2
）
2019
]
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：236引用：1難度：0.4
相似題
-
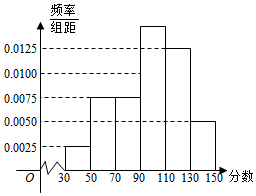1．某市舉行“中學生詩詞大賽”，分初賽和復賽兩個階段進行，規定：初賽成績大于90分的具有復賽資格，某校有800名學生參加了初賽，所有學生的成績均在區間（30，150]內，其頻率分布直方圖如圖．
（Ⅰ）求獲得復賽資格的人數；
（Ⅱ）從初賽得分在區間（110，150]的參賽者中，利用分層抽樣的方法隨機抽取7人參加學校座談交流，那么從得分在區間（110，130]與（130，150]各抽取多少人？
（Ⅲ）從（Ⅱ）抽取的7人中，選出3人參加全市座談交流，設X表示得分在區間（130，150]中參加全市座談交流的人數，求X的分布列及數學期望E（X）．發布：2024/12/29 13:30:1組卷：134引用：7難度：0.5 -
2．設離散型隨機變量X的分布列如表：
若離散型隨機變量Y=-3X+1，且E（X）=3，則（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 發布：2024/12/29 13:0:1組卷：199引用：6難度：0.5 -
3．從4名男生和2名女生中任選3人參加演講比賽，用X表示所選3人中女生的人數，則E（X）為（ ）
發布：2024/12/29 13:30:1組卷：139引用：6難度：0.7