在某次擊球訓練中，一同學將排球從離地高h=1.8m的A處以某一初速度水平擊出，球在空中的運動過程中（已知重力加速度g=10m/s2），求：
（1）在無阻力的情況下，如圖甲所示，將球從A點以v1=6m/s的初速度水平擊出，最終從B點沿圓弧切線落入地面中的一個圓弧形坑中，試求半徑OB與豎直方向夾角α；
（2）將圓弧坑填平后，如圖乙所示，在A點以v2=14m/s的初速度將排球水平擊出，球在空中的運動過程中受到水平恒定風力影響，落地前瞬間速度與水平方向成β=37°，已知sin37°=0.6，cos37°=0.8，求落地點距擊球點的水平距離；
（3）在（2）問的條件下，球在空中的運動過程中的最小速度大小。
【考點】平拋運動速度的計算；合運動與分運動的關系．
【答案】（1）半徑OB與豎直方向夾角為45°；
（2）落地點距擊球點的水平距離為6.6m；
（3）球在空中的運動過程中的最小速度大小為10m/s。
（2）落地點距擊球點的水平距離為6.6m；
（3）球在空中的運動過程中的最小速度大小為10m/s。
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/3 8:0:9組卷：80引用：2難度：0.5
相似題
-
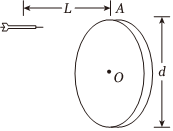1．如圖所示，一位同學做飛鏢游戲，已知圓盤的直徑為d,飛鏢距圓盤的水平距離為L。將飛鏢對準A點以初速度v0水平拋出，在飛鏢拋出的同時，圓盤以角速度ω繞垂直圓盤過盤心O的水平軸勻速轉動。要使飛鏢恰好擊中A點，則飛鏢的初速度和圓盤的角速度應滿足（ ）發布：2024/12/30 0:0:1組卷：46引用：4難度：0.6 -
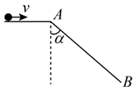2．如圖，在一個光滑水平面上以速度v運動的小球，到達A處時遇到一個足夠長的陡坡AB，已知AB與豎直線之間的夾角為α，重力加速度取g。則小球（ ）發布：2025/1/6 0:30:5組卷：92引用：2難度：0.6 -
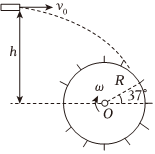3．如圖所示為某種水輪機的示意圖，水平管中流出的水流沖擊水輪機上的某擋板時，水流的速度方向剛好與水輪機上該擋板的線速度方向相同，水輪機圓盤穩定轉動時的角速度為ω，圓盤的半徑為R，水流沖擊某擋板時，該擋板和圓心連線與水平方向夾角為37°，水流速度與該擋板線速度相等，忽略擋板的大小，不計空氣阻力，則水從管口流出的速度v0大小為（ ）發布：2024/12/30 0:0:1組卷：61引用：5難度：0.7