證明：當AB是三個圓的公共弦，過A的不同于AB的任意一條直線確定相同的比XY：YZ，這里X是在第一個圓上不同于B的任意一點，而Y與Z是AX交其它兩個圓的交點（使Y標記在X與Z之間）．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：149引用：1難度：0.5

相似題

1．如圖，在矩形ABCD中，AB＜AD，以點A為圓心，線段AD的長為半徑畫弧，與BC邊交于點E，連接AE，過點D作DF⊥AE于點F．
（1）求證：DF=AB．
（2）連接BF，若BE=6，CE=3，求線段BF的長．
發布：2025/5/22 13:0:1組卷：759引用：2難度：0.5
解析
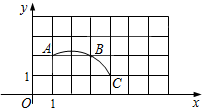2．如圖，在平面直角坐標系中，過格點A，B，C作一圓弧，則該弧的圓心的坐標為（　　）
A．（1，0） B．（2，0） C．（2.5，0） D．（2.5，1）
發布：2025/5/22 4:30:1組卷：144引用：3難度：0.7
解析
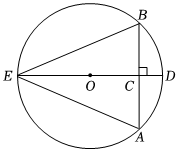3．如圖，在⊙O中，AB為弦，OC⊥AB于點C，交⊙O于點D，E，連接EA，EB，則圖中存在的相等關系有
（寫出兩組即可）．
發布：2025/5/22 13:30:1組卷：237引用：2難度：0.7
解析

相關試卷

1．如圖，在矩形ABCD中，AB＜AD，以點A為圓心，線段AD的長為半徑畫弧，與BC邊交于點E，連接AE，過點D作DF⊥AE于點F．（1）求證：DF=AB．（2）連接BF，若BE=6，CE=3，求線段BF的長．