問題：如圖①，在等邊三角形ABC內有一點P，且PA=2，PB=3，PC=1，求∠BPC的度數和等邊三角形ABC的邊長．
（1）李明的思路是：將△BPC繞點B逆時針旋轉60°，畫出旋轉后的圖形（如圖②），連接PP′，可得△P′PB是等邊三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可證），可得∠AP′B=150150°，所以∠BPC=∠AP′B=150150°，還可證得△ABP是直角三角形，進而求出等邊三角形ABC的邊長為 77，問題得到解決．
（2）探究并解決下列問題：如圖③，在正方形ABCD內有一點P，且PA=5，PB=2，PC=1．求∠BPC的度數和正方形ABCD的邊長．
PB
=
3
7
7
PA
=
5
PB
=
2
【答案】150；150；
7
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：279引用：1難度：0.5
相似題
-
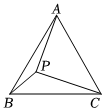1．如圖，在等邊△ABC中，AB=7，點P是△ABC內一點，且∠APC=90°，∠BPC=120°，則△APC的面積為 ．發布：2025/5/24 19:30:1組卷：153引用：1難度：0.5 -
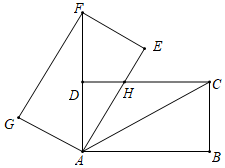2．如圖，將矩形ABCD繞點A旋轉至矩形AEFG的位置，此時點D恰好與AF的中點重合，AE交CD于點H，若BC=2，則HC的長為．3發布：2025/5/24 21:0:1組卷：122引用：2難度：0.6 -
3．如圖，在△ABC中，∠C=36°，將△ABC繞點A逆時針旋轉60°得到△AED，AD與BC交于點F，則∠AFC的度數為（ ）發布：2025/5/24 18:0:1組卷：520引用：6難度：0.9