如果一個四位自然數t的各個數位上的數字均不為0，且滿足千位數字與十位數字的和為9，百位數字與個位數字的差為1，那么稱t為“九一數”．把t的千位數字的2倍與個位數字的和記為P（t），百位數字的2倍與十位數字的和記為Q（t），令G（t）=2P（t）Q（t），當G（t）為整數時，則稱t為“整九一數”．若M=2000a+1000+100b+10c+d（其中1≤a≤4，1≤b≤9，1≤c≤9，1≤d≤9且a、b、c、d均為整數）是“整九一數”，則滿足條件的M的最大值為 75247524．
G
（
t
）
=
2
P
（
t
）
Q
（
t
）
【考點】整式的加減．
【答案】7524
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/10 5:30:2組卷：303引用：4難度：0.6
相似題
-
1．計算：
（1）3（a2-ab）-5（ab+2a2-1）；
（2）3x2-[5x-（-3）+3x2]．12x發布：2025/6/10 15:30:2組卷：1383引用：2難度：0.6 -
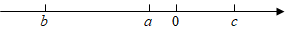2．實數a,b,c在數軸上的對應點如圖所示，化簡：．|a|+3（c-b）3-|a+b|+（a-c）2發布：2025/6/10 15:30:2組卷：139引用：6難度：0.7 -
3．如圖，把四張大小相同的長方形卡片（如圖1）按圖2、圖3兩種方式放在一個底面為長方形（長比寬多2cm）的盒底上，底面未被卡片覆蓋的部分用陰影表示，若記圖2中陰影部分的周長為C1，圖3中陰影部分的周長為C2，那么C1比C2大 cm.
發布：2025/6/11 2:30:2組卷：291引用：3難度：0.7