閱讀下面材料:
小聰遇到這樣一個問題:如圖1,∠AOB=α,請畫一個∠AOC,使∠AOC與∠BOC互補.
小聰是這樣思考的:首先通過分析明確射線OC在∠AOB的外部,畫出示意圖,如圖2所示:然后通過構造平角找到∠AOC的補角∠COD,
如圖3所示:進而分析要使∠AOC與∠BOC互補,則需∠BOC=∠COD.
因此,小聰找到了解決問題的方法:反向延長射線OA得到射線OD,利用量角器畫出∠BOD的平分線OC,這樣就得到了∠BOC與∠AOC互補.
(1)小聰根據自己的畫法寫出了已知和求證,請你完成證明:
已知:如圖3,點O在直線AD上,射線OC平分∠BOD.
求證:∠AOC與∠BOC互補.
(2)參考小聰的畫法,請在圖4中畫出一個∠AOH,使∠AOH與∠BOH互余.(保留畫圖痕跡)
(3)已知∠EPQ和∠FPQ互余,射線PM平分∠EPQ,射線PN平分∠FPQ.若∠EPQ=β(0°<β<90°),直接寫出銳角∠MPN的度數是45°或|β-45°|45°或|β-45°|.
【答案】45°或|β-45°|
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/31 4:0:1組卷:1038引用:2難度:0.5
相似題
-
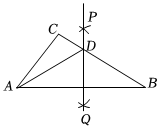 1.如圖,在△ABC中,分別以點A和點B為圓心,大于的長為半徑畫弧,兩弧相交于點P、Q,作直線PQ交AB于點D,連接AD,若△ABC的周長為15,AB=6,則△ADC的周長為 .12AB發布:2025/6/1 13:30:1組卷:97引用:2難度:0.6
1.如圖,在△ABC中,分別以點A和點B為圓心,大于的長為半徑畫弧,兩弧相交于點P、Q,作直線PQ交AB于點D,連接AD,若△ABC的周長為15,AB=6,則△ADC的周長為 .12AB發布:2025/6/1 13:30:1組卷:97引用:2難度:0.6 -
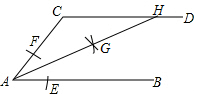 2.如圖,AB∥CD,以點A為圓心,小于AC的長為半徑作圓弧,分別交AB,AC于E,F兩點,再分別以E,F為圓心,以大于EF長為半徑作圓弧,兩條弧交于點G,作射線AG交CD于點H,若∠C=120°,則∠AHD=( )12
2.如圖,AB∥CD,以點A為圓心,小于AC的長為半徑作圓弧,分別交AB,AC于E,F兩點,再分別以E,F為圓心,以大于EF長為半徑作圓弧,兩條弧交于點G,作射線AG交CD于點H,若∠C=120°,則∠AHD=( )12A.120° B.30° C.150° D.60° 發布:2025/6/1 14:30:2組卷:338引用:6難度:0.9 -
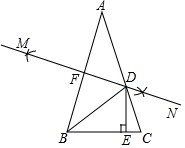 3.如圖,在△ABC中,AB=AC,∠A=36°,分別以A和B為圓心,大于AB的長為半徑作弧,兩弧相交于M,N兩點,作直線MN分別交AB、AC于點F、D,作DE⊥BC于E.有下面三個結論:12
3.如圖,在△ABC中,AB=AC,∠A=36°,分別以A和B為圓心,大于AB的長為半徑作弧,兩弧相交于M,N兩點,作直線MN分別交AB、AC于點F、D,作DE⊥BC于E.有下面三個結論:12
①BD平分∠ABC
②DE=DF
③BC+CD=2AF
其中,正確的結論的個數是( )A.3 B.2 C.1 D.0 發布:2025/6/1 12:30:1組卷:129引用:3難度:0.7


