定義：有限非空數(shù)集Ω的所有元素的“乘積”稱為數(shù)集Ω的“積數(shù)”，例如：集合Ω={1，2，3}，其“積數(shù)”=1×2×3=6．
（1）若有限數(shù)集A={a1，a2，a3}，求證：集合A的所有非空子集的“積數(shù)”之和SA滿足SA=（1+a1）（1+a2）（1+a3）-1；
（2）根據(jù)（1）的結(jié)論，對于有限非空數(shù)集A={a1，a2，……，an}（n∈N*，n≥2），記集合A的所有非空子集的“積數(shù)”之和Sn，試寫出Sn的表達(dá)式，并利用“數(shù)學(xué)歸納法”給予證明；
（3）若有限集Ω={12，13，14，…，1100}，
1）試求由Ω中所有奇數(shù)個元素構(gòu)成的非空子集的“積數(shù)”之和S奇數(shù)；
2）試求由Ω中所有偶數(shù)個元素構(gòu)成的非空子集的“積數(shù)”之和S偶數(shù)．
Ω
=
{
1
2
，
1
3
，
1
4
，…，
1
100
}
【考點】數(shù)學(xué)歸納法證明命題．
【答案】（1）證明見解析；
（2）Sn=（1+a1）（1+a2）（1+a3）…（1+an）-1，n∈N*，證明見解析；
（3）1）；
2）．
（2）Sn=（1+a1）（1+a2）（1+a3）…（1+an）-1，n∈N*，證明見解析；
（3）1）
S
奇數(shù)
=
5049
200
2）
S
偶數(shù)
=
4851
200
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：66引用：1難度：0.4
相似題
-
1．在數(shù)列{an}中，
．a1=1，an+1=2an2+an（n∈N*）
（Ⅰ）分別求出a2，a3，a4，并根據(jù)上述結(jié)果猜想這個數(shù)列的通項公式；
（Ⅱ）請用數(shù)學(xué)歸納法證明（Ⅰ）中的猜想．發(fā)布：2024/12/28 23:30:2組卷：44引用：2難度：0.6 -
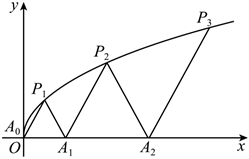2．如圖，P1（x1，y1），P2（x2，y2），?，Pn（xn，yn）（0＜y1＜y2＜?＜yn）是曲線C：y2=3x（y≥0）上的n個點，點Ai（ai，0）（i=1，2，3，?，n）在x軸的正半軸上，且△Ai-1AiPi是正三角形（A0是坐標(biāo)原點）．
（1）求a1、a2、a3的值及數(shù)列{an}的遞推公式；
（2）猜想點An（an，0）的橫坐標(biāo)an關(guān)于n的表達(dá)式，并用數(shù)學(xué)歸納法證明．發(fā)布：2024/7/13 8:0:9組卷：52引用：2難度：0.5 -
3．已知點Pn（an，bn） 滿足an+1=anbn+1，bn+1=
，且點P1的坐標(biāo)為（1，-1）．bn1-4a2n
（1）求過點P1、P2的直線l的方程；
（2）試用數(shù)學(xué)歸納法證明：對于任意n∈N，n≥1，點Pn都在（1）中的直線l上；
（3）試求數(shù)列{an}、{bn}的通項公式．發(fā)布：2024/8/15 5:0:1組卷：160引用：1難度：0.4