在學習角平分性質的過程中，首先要探究角平分線的作圖方法，請同學們閱讀下列材料，回答問題：
已知：∠AOB．
求作：∠AOB的平分線．
作法：（I）以點O為圓心，適當長為半徑畫弧，交OA于點M，交OB于點N．
（II）分別以點M、N為圓心，大于12MN的長為半徑畫弧，兩弧在∠AOB的內部相交于點C．
（Ⅲ）畫射線OC，射線OC即為所求．
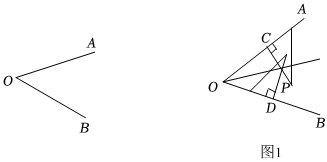
（1）請你按照上面做法畫出圖形．
（2）OC就是∠AOB的角平分線的依據是 SSSSSS．
課后老師留了一道思考題，還有沒有其他作角平分線的方法（不限于圓規和直尺）？下面是一位同學給出的方法：
（3）如圖1，在已知的∠AOB上，分別取OC=OD，再分別過點C，D作OA，OB的垂線，交點為P，畫射線OP，則OP平分∠AOB．請你幫這位同學證明：OP平分∠AOB．
1
2
【考點】三角形綜合題．
【答案】SSS
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/6 6:0:10組卷：44引用：2難度：0.3
相似題
-
1．在平面直角坐標系中，點A、B、C的坐標分別為（m,0），（2，-4），（n,0），且m,n滿足方程（m-2）xn-4+
=0為二元一次方程．ym2-3
（1）求A、C的坐標；
（2）若點D為y軸正半軸上的一個動點．
①如圖1，已知∠DAO=∠ACB，∠ADO與∠ACB的角平分線交于點P，求∠P的度數；
②如圖2，連接BD，交x軸于點E．若S△ADE≤S△BCE成立．設動點D坐標為（0，a），求a的取值范圍．
發布：2025/6/8 0:30:1組卷：83引用：1難度：0.1 -
2．在平面直角坐標系中，A（a,0），C（b,2），且滿足（a+b）2+|a-b+4|=0，過C作CB⊥x軸于B．
（1）如圖1，求△ABC的面積．
（2）如圖2，若過B作BD∥AC交y軸于D，在△ABC內有一點E，連接AE、DE，若∠CAE+∠BDE=∠EAO+∠EDO，求∠AED的度數．
（3）如圖3，在（2）的條件下，DE與x軸交于點M，AC與y軸交于點F，作△AME的角平分線MP，在PE上有一點Q，連接QM，∠EAM+2∠PMQ=45°，當AE=mAM，FO=2QM時，求點E的縱坐標（用含m的代數式表示）．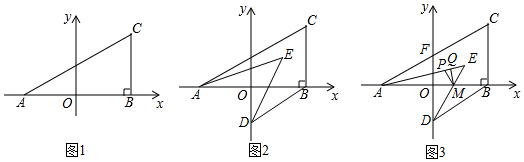
發布：2025/6/7 23:0:2組卷：189引用：2難度：0.2 -
3．已知線段AB⊥l于點B，點D在直線l上，分別以AB、AD為邊作等邊三角形ABC和等邊三角形ADE，直線CE交直線l于點F．
（1）當點F在線段BD上時，如圖①，直接寫出DF，CE，CF之間的關系 ．
（2）當點F在線段BD的延長線上時，如圖②，當點F在線段DB的延長線上時，如圖③，請分別寫出線段DF、CE、CF之間的數量關系，在圖②、圖③中選一個進行證明．
（3）在（1）、（2）的條件下，若BD=2BF，EF=6，請直接寫出CF的值．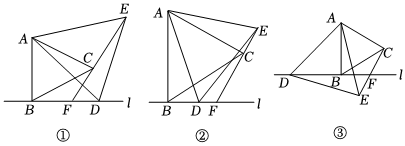
發布：2025/6/8 2:0:5組卷：424引用：2難度：0.1