點P為平面內任意一點，若△ABC上存在點Q，滿足PQ=1，則稱點P為△ABC的等距離點．在平面直角坐標系xOy中，點A（t-4，1）與點B關于過點（t,0）且垂直于x軸的直線對稱．
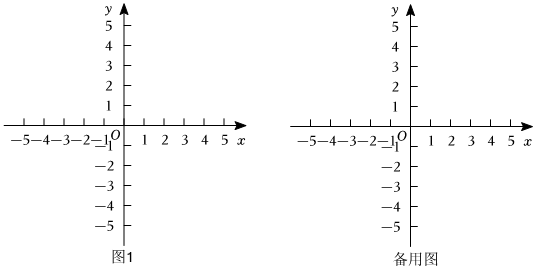
（1）以AB為底邊作等腰△ABC，
①t=0，點B的坐標為 （4，1）（4，1）；
②當t=1，且底邊AB上的高為3時，點C的坐標為 （1，4）或（1，-2）（1，4）或（1，-2）．
（2）以AB為斜邊作等腰直角△ABD（點D在線段AB的上方）
①直線m過點（0，b）且與x軸平行，若直線m上存在△ABD的等距離點，試畫圖說明b的取值范圍；
②已知點M（5，3），N（5+2，3），若線段MN上的所有點均為△ABD的等距離點，請直接寫出t的取值范圍．（提示：若等腰直角三角形的腰長為1，則斜邊長為2．）
2
2
【考點】三角形綜合題．
【答案】（4，1）；（1，4）或（1，-2）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/25 4:0:1組卷：88引用：3難度：0.1
相似題
-
1．如圖，在△ABC中，∠ACB=90°，CA=CB，∠MCN=45°，射線CM交直線AB于點P，過點A作AD⊥CM于點D，直線AD交直線CN于點E，連接BE．
（1）當點P在線段AB上時，如圖①，求證：AD+BE=DE；
（2）當點P在BA的延長線上時，如圖②；當點P在AB的延長線上時，如圖③，線段AD，DE，BE之間又有怎樣的數量關系？直接寫出你的猜想，不必證明．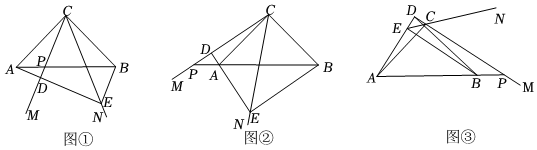
發布：2025/5/25 19:30:2組卷：79引用：1難度：0.3 -
2．某興趣小組探索等腰三角形中線段比值問題，部分探索活動如下：
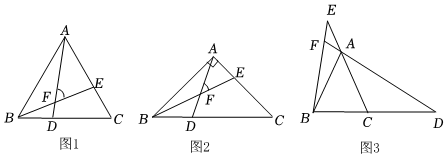
（1）如圖1，在△ABC中，AB=AC，∠ABC=60°，D，E分別是BC，AC邊上的點，∠AFE=∠ABC，則的值為 ．BEAD
（2）如圖2，在△ABC中，AB=AC，∠ABC=45°，D，E分別是BC，AC邊上的點，∠AFE=∠ABC，請你猜想的值，并給出證明；BEAD
（3）如圖3，在△ABC中，AB=AC，，D，E分別是BC，CA邊延長線上的點，∠DFB=∠ABC，請直接寫出cos∠ABC=512的值．BEAD發布：2025/5/26 0:0:1組卷：153引用：1難度：0.4 -
3．如圖①，在△ABC中，∠ABC=90°，過點B作直線BD交邊AC于點D，過點A作AE⊥BD，垂足為點E，過點C作CF⊥BD，垂足為點F，點O為AC的中點，連結OE、OF．
【證明推斷】求證：OE=OF．
小明給出的思路：先分別延長EO、CF交于點M，再證明△AEO≌△CMO．請你根據小明的思路完成證明過程．
【拓展應用】如圖②，當BC=4AB，∠DBC=45°時，解決下列問題：
（1）∠EFO的大小為 度．
（2）的值為 ．ODOC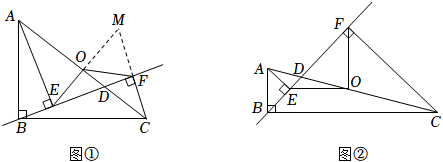
發布：2025/5/25 18:0:1組卷：179引用：2難度：0.4