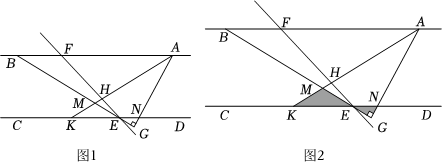
如圖1,AB∥CD,點E,F分別在直線CD,AB上,∠BEC=2∠BEF,過點A作AG⊥BE的延長線交于點G,交CD于點N,AK平分∠BAG,交EF于點H,交BE于點M.
(1)直接寫出∠AHE,∠FAH,∠HFA之間的關系:∠AHE=∠FAH+∠HFA∠AHE=∠FAH+∠HFA;
(2)若∠BEF=12∠BAK,求∠AHE的度數.
(3)如圖2,在(2)的條件下,將三角形KHE繞著點E以每秒5°的速度逆時針旋轉,旋轉時間為t,當KE邊與射線ED重合時停止轉動.則在旋轉過程中,當三角形KHE的其中一邊與三角形ENG的某一邊平行時,直接寫出此時t的值.
∠
BEF
=
1
2
∠
BAK
【考點】平行線的判定與性質.
【答案】∠AHE=∠FAH+∠HFA
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/5 8:0:8組卷:346引用:3難度:0.4