綜合與實踐
問題情境：數學活動課上，王老師出示了一個問題：
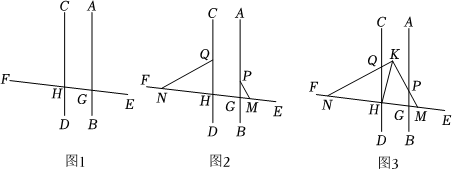
如圖1，直線CD∥直線AB，直線FE分別交直線CD、直線AB于點H、G，
求證：∠BGE+∠CHG=180°．
獨立思考：（1）請解答王老師提出的問題．
實踐探究：（2）在原有問題條件不變的情況下，王老師提出新問題，請你解答．
“如圖2，點N在射線HF上，點M在射線GE上，點Q在射線HC上，點P在射線GA上，連結NQ、MP，且∠NQC+∠APM=270°，探究直線NQ與直線MP之間的位置關系并說明理由；”
問題解決：（3）數學活動小組同學對上述問題進行特殊化研究之后發現，在（2）的條件下，連接KH，使KH平分∠NKM，∠KHE+∠CHE=180°，若給出∠FHC與∠APK一定的數量關系，則圖3中所有已經用字母標記的角中，有些角是可以求出來的，該小組提出下面的問題，請你解答．
“如圖3，若

∠

FHC

∠

APK

=

17

7

，求∠PMH的度數并說明理由．”