我們已經學習了利用配方法解一元二次方程，其實配方法還有其他重要應用，例如：試求二次三項式x2+4x+5最小值．
解：x2+4x+5=x2+4x+4+1=（x+2）2+1，
∵（x+2）2≥0，（x+2）2+1≥1，
∴x2+4x+5≥1，即x2+4x+5的最小值是1．
試利用“配方法”解決下列問題：
（1）已知y=-x2-8x+14求y的最大（或最小）值．
（2）比較代數式2x2+3x-5與3x2-x+1的大小，并說明理由．
（3）知識遷移：
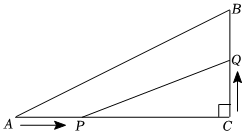
如圖，在Rt△ABC中，∠C=90°，AC=8cm,BC=6cm,點P在AC邊上以2cm/s的速度從點A向C移動，點Q在CB邊上以1cm/s的速度從點C向點B移動．若點P，Q同時出發，且當一點移動到終點時，另一點也隨之停止，設四邊形APQB的面積為S cm2運動時間為t秒，求S的最小值．
【答案】（1）30；（2）2x2+3x-5＜3x2-x+1；（3）20．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/7 1:0:8組卷：285引用：1難度：0.2