數學問題:計算1m+1m2+1m3+…+1mn(其中m,n都是正整數,且m≥2,n≥1).
探究問題:為解決上面的數學問題,我們運用數形結合的思想方法,通過不斷地分割一個面積為1的正方形,把數量關系和幾何圖形巧妙地結合起來,并采取一般問題特殊化的策略來進行探究.
探究一:計算12+122+123+…+12n.
第1次分割,把正方形的面積二等分,其中陰影部分的面積為12;
第2次分割,把上次分割圖中空白部分的面積繼續二等分,陰影部分的面積之和為12+122;
第3次分割,把上次分割圖中空白部分的面積繼續二等分,…;
…
第n次分割,把上次分割圖中空白部分的面積最后二等分,所有陰影部分的面積之和為12+122+123+…+12n,最后空白部分的面積是12n.
根據第n次分割圖可得等式:12+122+123+…+12n=1-12n.
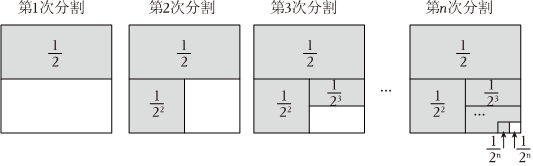
探究二:計算13+132+133+…+13n.
第1次分割,把正方形的面積三等分,其中陰影部分的面積為23;
第2次分割,把上次分割圖中空白部分的面積繼續三等分,陰影部分的面積之和為23+232;
第3次分割,把上次分割圖中空白部分的面積繼續三等分,…;
…
第n次分割,把上次分割圖中空白部分的面積最后三等分,所有陰影部分的面積之和為23+232+233+…+23n,最后空白部分的面積是13n.
根據第n次分割圖可得等式:23+232+233+…+23n=1-13n,
兩邊同除以2,得13+132+133+…+13n=12-12×3n.
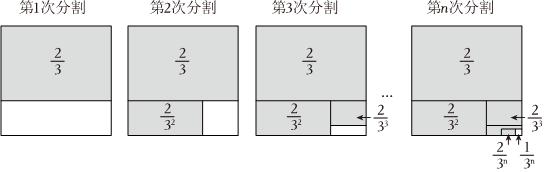
探究三:計算14+142+143+…+14n.
(仿照上述方法,只畫出第n次分割圖,在圖上標注陰影部分面積,并寫出探究過程)

解決問題:計算1m+1m2+1m3+…+1mn.
(只需畫出第n次分割圖,在圖上標注陰影部分面積,并完成以下填空)
根據第n次分割圖可得等式:34+342+343+…+34n=1-14n34+342+343+…+34n=1-14n,
所以,1m+1m2+1m3+…+1mn=1m-1-1(m-1)×mn1m-1-1(m-1)×mn.
拓廣應用:計算5-15+52-152+53-153+…+5n-15n.
1
m
1
m
2
1
m
3
1
m
n
1
2
1
2
2
1
2
3
1
2
n
1
2
1
2
1
2
2
1
2
1
2
2
1
2
3
1
2
n
1
2
n
1
2
1
2
2
1
2
3
1
2
n
1
2
n
1
3
1
3
2
1
3
3
1
3
n
2
3
2
3
2
3
2
2
3
2
3
2
2
3
3
2
3
n
1
3
n
2
3
2
3
2
2
3
3
2
3
n
1
3
n
1
3
1
3
2
1
3
3
1
3
n
1
2
1
2
×
3
n
1
4
1
4
2
1
4
3
1
4
n
1
m
1
m
2
1
m
3
1
m
n
3
4
3
4
2
3
4
3
3
4
n
1
4
n
3
4
3
4
2
3
4
3
3
4
n
1
4
n
1
m
1
m
2
1
m
3
1
m
n
1
m
-
1
1
(
m
-
1
)
×
m
n
1
m
-
1
1
(
m
-
1
)
×
m
n
5
-
1
5
5
2
-
1
5
2
5
3
-
1
5
3
5
n
-
1
5
n
【考點】作圖—應用與設計作圖;規律型:圖形的變化類.
【答案】+++…+=1-;-
3
4
3
4
2
3
4
3
3
4
n
1
4
n
1
m
-
1
1
(
m
-
1
)
×
m
n
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/18 22:0:2組卷:1924引用:31難度:0.1
相似題
-
 1.線段、角、三角形、和圓都是幾何研究的基本圖形,請用這些圖形設計表現客觀事物的圖案,每幅圖可以由一種圖形組成,也可以由兩種或三種圖案組成,但總數不得超過三個,并且為每幅圖案命名,命名要求與畫面相符(如圖的示例)(不少于2幅)發布:2025/6/19 3:0:1組卷:23引用:4難度:0.3
1.線段、角、三角形、和圓都是幾何研究的基本圖形,請用這些圖形設計表現客觀事物的圖案,每幅圖可以由一種圖形組成,也可以由兩種或三種圖案組成,但總數不得超過三個,并且為每幅圖案命名,命名要求與畫面相符(如圖的示例)(不少于2幅)發布:2025/6/19 3:0:1組卷:23引用:4難度:0.3 -
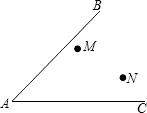 2.如圖,AC、AB是兩條筆直的交叉公路,M、N是兩個實習點,現欲建一個茶水供應站,使得此茶水供應站到公路兩邊的距離相等,且離M、N兩個實習點的距離也相等,此茶水站應建在何處?發布:2025/6/19 3:0:1組卷:143引用:8難度:0.3
2.如圖,AC、AB是兩條筆直的交叉公路,M、N是兩個實習點,現欲建一個茶水供應站,使得此茶水供應站到公路兩邊的距離相等,且離M、N兩個實習點的距離也相等,此茶水站應建在何處?發布:2025/6/19 3:0:1組卷:143引用:8難度:0.3 -
3.如圖,正方形網格中的每個小正方形邊長都是1,每個小格的頂點叫做格點,以格點為頂點分別按下列要求畫三角形(涂上陰影).
(1)在圖1中,畫一個三角形,使它的三邊長都是有理數;
(2)在圖2,圖3中,分別畫一個直角三角形,使它的三邊長都是無理數.(兩個三角形不全等) 發布:2025/6/19 1:30:1組卷:450引用:42難度:0.5
發布:2025/6/19 1:30:1組卷:450引用:42難度:0.5


