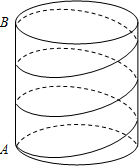
如圖，圓柱底面半徑為2πcm,高為9cm,點A，B分別是圓柱兩底面圓周上的點，且A，B在同一條豎直直線上，用一根棉線從A點順著圓柱側(cè)面繞3圈到B點，則這根棉線的長度最短為 1515cm.
2
π
【考點】平面展開-最短路徑問題．
【答案】15
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/1 11:30:2組卷：608引用：3難度：0.5
相似題
-
1．如圖，已知圓柱底面周長為6cm,圓柱高為2cm,在圓柱的側(cè)面上，過點A和點C嵌有一圈金屬絲，則這圈金屬絲的周長最小為cm.發(fā)布：2025/6/2 21:30:9組卷：1798引用：10難度：0.6 -
2．如圖，直線l是一條河，P，Q兩地在直線l的同側(cè)，欲在l上的某點M處修建一個水泵站，分別向P，Q兩地供水．現(xiàn)有如下四種鋪設方案，則鋪設的管道最短的方案是（ ）發(fā)布：2025/6/3 2:0:7組卷：66引用：2難度：0.7 -
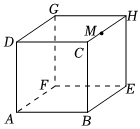3．如圖是一個棱長為30cm的無蓋正方體盒子，點M在棱CH上，且CM=10cm.一只螞蟻如果要沿著正方體的側(cè)面從點A爬到點M，需要爬行的最短路程是多少？發(fā)布：2025/6/3 6:0:2組卷：54引用：1難度：0.7