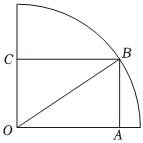
如圖，在半徑為4m的四分之一圓（O為圓心）鋁皮上截取一塊矩形材料OABC，其中點B在圓弧上，點A，C在兩半徑上，現將此矩形鋁皮OABC卷成一個以AB為母線的圓柱形罐子的側面（不計剪裁和拼接損耗），設矩形的邊長AB=x m,圓柱的體積為Vm³．
（1）求出體積V關于x的函數關系式，并指出定義域；
（2）當x為何值時，才能使做出的圓柱形罐子的體積V最大？最大體積是多少？

【答案】（1）

，定義域為{x|0＜x＜4}；
（2）當

m時，圓柱形罐子的體積V最大，最大體積是

m³．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/12/29 8:0:12組卷：39引用：12難度：0.5

相似題

1．已知函數
f
（
x
）
=
ln
2
+
x
2
-
x
+
1
，若關于x的不等式
f
（
k
e
x
）
+
f
（
-
1
2
x
）
＞
2
對任意x∈（0，2）恒成立，則實數k的取值范圍（　　）
A．（
1
2
e
，+∞） B．（
1
2
e
，
2
e
2
） C．（
1
2
e
，
2
e
2
] D．（
2
e
2
，1]
發布：2025/1/5 18:30:5組卷：297引用：2難度：0.4
解析
2．已知函數f（x）=
e
x
-
a
x
2
1
+
x
．
（1）若a=0，討論f（x）的單調性．
（2）若f（x）有三個極值點x₁，x₂，x₃．
①求a的取值范圍；
②求證：x₁+x₂+x₃＞-2．
發布：2024/12/29 13:0:1組卷：190引用：2難度：0.1
解析
3．已知函數f（x）=ax³+x²+bx（a,b∈R）的圖象在x=-1處的切線斜率為-1，且x=-2時，y=f（x）有極值．
（1）求f（x）的解析式；
（2）求f（x）在[-3，2]上的最大值和最小值．
發布：2024/12/29 12:30:1組卷：48引用：4難度：0.5
解析

相關試卷

1．已知函數f（x）=ln2+x2-x+1，若關于x的不等式f（kex）+f（-12x）＞2對任意x∈（0，2）恒成立，則實數k的取值范圍（ ）