早在公元前古希臘數學家歐幾里得就發現了垂徑定理，即垂直于弦的直徑平分弦．阿基米德從中看出了玄機并提出：如果條件中的弦變成折線段，仍然有類似的結論．
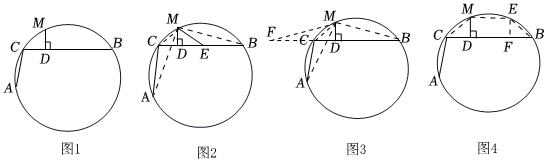
某數學興趣小組對此進行了探究，如圖1，AC和BC是⊙O的兩條弦（即折線段ACB是圓的一條折弦），BC＞AC，M是?ACB的中點，過點M作MD⊥BC，垂足為D，小明通過度量AC、CD、DB的長度，發現點D平分弦ACB，即BD=AC+CD．小麗和小軍改變折弦的位置發現BD=AC+CD仍然成立，于是三位同學都嘗試進行了證明：
小軍采用了“截長法”（如圖2），在BD上截取BE，使得BE=AC，…
小麗則采用了“補短法”（如圖3），延長BC至F，使CF=AC，…
小明采用了“平行線法”（如圖4），過M點作ME∥BC，交圓于點E，過點E作EF⊥BC，…
（1）請你任選一位同學的方法，并完成證明；
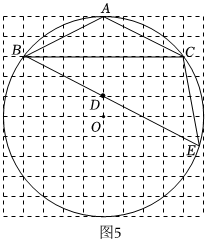
（2）如圖5，在網格圖中，每個小正方形邊長均為1，△ABC內接于⊙O（A、B、C均是格點），點A、D關于BC對稱，連接BD并延長交⊙O于點E，連接CE．
①請作直線l,使得直線l平分△BCE的周長；
②求△BCE的周長．
?
ACB
【考點】圓的綜合題．
【答案】（1）證明過程見解答部分；
（2）①圖形見解答部分；
②△BCE的周長為：8+．
（2）①圖形見解答部分；
②△BCE的周長為：8+
32
5
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/7 8:0:9組卷：292引用：4難度：0.2
相似題
-
1．若AC=4，以點C為圓心，2為半徑作圓，點P為該圓上的動點，連接AP．
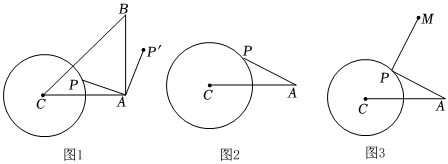
（1）如圖1，取點B，使△ABC為等腰直角三角形，∠BAC=90°，將點P繞點A順時針旋轉90°得到AP′．
①點P'的軌跡是 （填“線段”或者“圓”）；
②CP'的最小值是 ；
（2）如圖2，以AP為邊作等邊△APQ（點A、P、Q按照順時針方向排列），在點P運動過程中，求CQ的最大值．
（3）如圖3，將點A繞點P逆時針旋轉90°，得到點M，連接PM，則CM的最小值為 ．發布：2025/5/24 11:30:1組卷：521引用：2難度：0.3 -
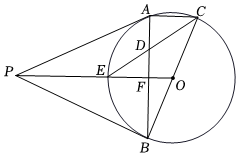2．如圖，PA、PB是⊙O的切線，切點分別為A、B，BC是⊙O的直徑，PO交⊙O于E點，連接AB交PO于F，連接CE交AB于D點．下列結論：①PA=PB；②OP⊥AB；③CE平分∠ACB；④；⑤E是△PAB的內心；⑥△CDA≌△EDF．其中一定成立的有（ ）個．OF=12AC發布：2025/5/24 12:0:1組卷：489引用：2難度：0.3 -
3．如圖1，CD是⊙O的弦，半徑OA⊥CD，垂足為B，過點C作⊙O的切線l.
（1）若點E在⊙O上，且=?CE，連接OE．?CA
①連接AE，求證：AE∥l；
②如圖2，若B是OA的中點，連接OD，求證：DE是⊙O的直徑；
（2）如圖3，過點B作BF⊥l,垂足為F，若⊙O的半徑是4，求BC-BF的最大值．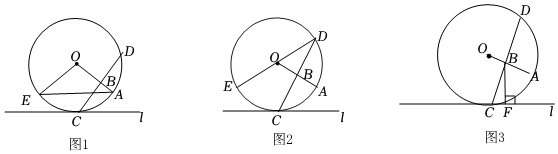
發布：2025/5/24 11:0:1組卷：345引用：3難度：0.3