 問題情境:將一副直角三角板(Rt△ABC和Rt△DEF)按圖1所示的方式擺放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中點,點D與點O重合,DF⊥AC于點M,DE⊥BC于點N,試判斷線段OM與ON的數量關系,并說明理由.
問題情境:將一副直角三角板(Rt△ABC和Rt△DEF)按圖1所示的方式擺放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中點,點D與點O重合,DF⊥AC于點M,DE⊥BC于點N,試判斷線段OM與ON的數量關系,并說明理由.
探究展示:小宇同學展示出如下正確的解法:
解:OM=ON,證明如下:
連接CO,則CO是AB邊上中線,
∵CA=CB,∴CO是∠ACB的角平分線.(依據1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依據2)
反思交流:
(1)上述證明過程中的“依據1”和“依據2”分別是指:
依據1:等腰三角形的三線合一(等腰三角形頂角的平分線、底邊上的中線、底邊上的高互相重合)等腰三角形的三線合一(等腰三角形頂角的平分線、底邊上的中線、底邊上的高互相重合);
依據2:角平分線上的點到角的兩邊的距離相等角平分線上的點到角的兩邊的距離相等.
(2)你有與小宇不同的思考方法嗎?請寫出你的證明過程.
拓展延伸:
(3)將圖1中的Rt△DEF沿著射線BA的方向平移至如圖2所示的位置,使點D落在BA的延長線上,FD的延長線與CA的延長線垂直相交于點M,BC的延長線與DE垂直相交于點N,連接OM、ON,試判斷線段OM、ON的數量關系與位置關系,并寫出證明過程.
【答案】等腰三角形的三線合一(等腰三角形頂角的平分線、底邊上的中線、底邊上的高互相重合);角平分線上的點到角的兩邊的距離相等
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:2246引用:12難度:0.3
相似題
-
 1.如圖,在△ABC中,∠BAC=90°,延長BA到點D,使AD=AB,點E、F分別為BC、AC的中點,請你在圖中找出一組相等關系,使其滿足上述所有條件,并加以證明.12發布:2025/1/24 8:0:2組卷:4引用:1難度:0.5
1.如圖,在△ABC中,∠BAC=90°,延長BA到點D,使AD=AB,點E、F分別為BC、AC的中點,請你在圖中找出一組相等關系,使其滿足上述所有條件,并加以證明.12發布:2025/1/24 8:0:2組卷:4引用:1難度:0.5 -
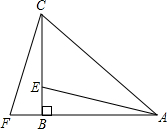 2.如圖,在△ABC中,AB=CB,∠ABC=90°,F為AB延長線上一點,點E在線段BC上,且AE=CF.
2.如圖,在△ABC中,AB=CB,∠ABC=90°,F為AB延長線上一點,點E在線段BC上,且AE=CF.
求證:∠AEB=∠CFB.發布:2025/1/24 8:0:2組卷:454引用:4難度:0.7 -
 3.如圖,在Rt△ABC中,∠C=∠BED=90°,且CD=DE,AD=BD,則∠B=.發布:2025/1/28 8:0:2組卷:10引用:0難度:0.7
3.如圖,在Rt△ABC中,∠C=∠BED=90°,且CD=DE,AD=BD,則∠B=.發布:2025/1/28 8:0:2組卷:10引用:0難度:0.7


