如圖1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8.點P在線段AB上以每秒2個單位的速度由點A向點B運動,同時,點Q在線段BD上由B點向點D運動.它們的運動時間為t(s).

(1)若點Q的運動速度與點P的運動速度相等,當t=2時,△ACP與△BPQ是否全等,請說明理由,并判斷此時線段PC和線段PQ的位置關系;
(2)如圖2,將圖1中的“AC⊥AB,BD⊥AB”改為“∠CAB=∠DBA=60°”,其他條件不變.設點Q的運動速度為每秒x個單位,是否存在實數x,使得△ACP與△BPQ全等?若存在,求出相應的x,t的值;若不存在,請說明理由.
【考點】全等三角形的判定;含30度角的直角三角形.
【答案】(1)△ACP≌△BPQ,PC⊥PQ;
(2)
或
.
(2)
t = 2 |
x = 2 |
t = 3 |
x = 8 3 |
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:799引用:7難度:0.4
相似題
-
 1.如圖,如果AD∥BC,AD=BC,AC與BD相交于O點,則圖中的全等三角形一共有( )
1.如圖,如果AD∥BC,AD=BC,AC與BD相交于O點,則圖中的全等三角形一共有( )A.3對 B.4對 C.5對 D.6對 發布:2025/6/17 6:30:2組卷:2432引用:10難度:0.9 -
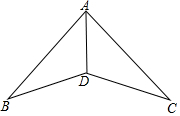 2.如圖,有下列條件:①BD=DC,AB=AC;②∠ADB=∠ADC,∠B=∠C;③∠B=∠C,∠BAD=∠CAD;④∠B=∠C,BD=DC其中,不能證明△ABD≌△ACD的是(填序號)發布:2025/6/17 4:30:1組卷:410引用:4難度:0.9
2.如圖,有下列條件:①BD=DC,AB=AC;②∠ADB=∠ADC,∠B=∠C;③∠B=∠C,∠BAD=∠CAD;④∠B=∠C,BD=DC其中,不能證明△ABD≌△ACD的是(填序號)發布:2025/6/17 4:30:1組卷:410引用:4難度:0.9 -
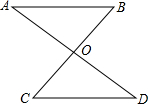 3.如圖所示,AB∥CD,AO=DO.求證:△AOB≌△DOC.發布:2025/6/17 6:0:2組卷:872引用:3難度:0.7
3.如圖所示,AB∥CD,AO=DO.求證:△AOB≌△DOC.發布:2025/6/17 6:0:2組卷:872引用:3難度:0.7


