為落實“雙減”，老師布置了一項這樣的課后作業：
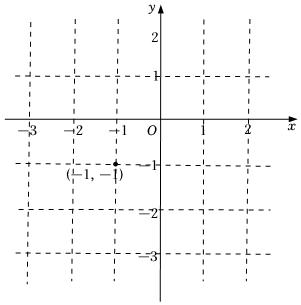
二次函數的圖象經過點（-1，-1），且不經過第一象限，寫出滿足這些條件的一個函數表達式．
【觀察發現】
請完成作業，并在直角坐標系中畫出大致圖象．
【思考交流】
小亮說：“滿足條件的函數圖象的對稱軸一定在y軸的左側．”
小瑩說：“滿足條件的函數圖象一定在x軸的下方．”
你認同他們的說法嗎？若不認同，請舉例說明．
【概括表達】
小博士認為這個作業的答案太多，老師不方便批閱，于是探究了二次函數y=ax2+bx+c的圖象與系數a,b,c的關系，得出了提高老師作業批閱效率的方法．
請你探究這個方法，寫出探究過程．
【考點】二次函數綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/7 8:0:9組卷：1108引用：3難度：0.4
相似題
-
1．在平面直角坐標系xOy中，拋物線y=
x2+bx+c過點A（-2，-1），B（0，-3）．12
（1）求拋物線的解析式；
（2）平移拋物線，平移后的頂點為P（m,n）（m＞0）．
ⅰ．如果S△OBP=3，設直線x=k,在這條直線的右側原拋物線和新拋物線均呈上升趨勢，求k的取值范圍；
ⅱ．點P在原拋物線上，新拋物線交y軸于點Q，且∠BPQ=120°，求點P的坐標．發布：2025/5/24 1:0:1組卷：3109引用：3難度：0.4 -
2．如圖1，拋物線y=ax2+3ax（a為常數，a＜0）與x軸交于O，A兩點，點B為拋物線的頂點，點D是線段OA上的一個動點，連接BD并延長與過O，A，B三點的⊙P相交于點C，過點C作⊙P的切線交x軸于點E．
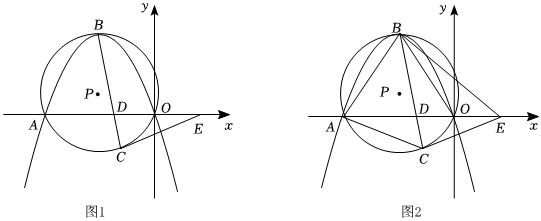
（1）①求點A的坐標；②求證：CE=DE；
（2）如圖2，連接AB，AC，BE，BO，當，∠CAE=∠OBE時，a=-233
①求證：AB2=AC?BE；②求的值．1OD-1OE發布：2025/5/24 1:0:1組卷：575引用：1難度：0.3 -
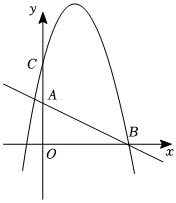3．如圖，直線與x軸、y軸分別交于點B、A，拋物線y=-x2+bx+c經過點B，與y軸交于點C（0，4）．y=-12x+2
（1）求拋物線的函數表達式；
（2）點P是x軸上方拋物線上的動點，過點P作PD⊥x軸于點D，若以點P、D、B為頂點的三角形與△AOB相似，求點P的坐標．發布：2025/5/24 1:0:1組卷：358引用：2難度：0.3