小明發現這樣一個規律：兩個頂角相等的等腰三角形，如果具有公共的頂角的頂點，并把它們的底角頂點連接起來，則形成一組全等三角形，小明把具有這個規律的圖形稱為“手拉手”圖形．
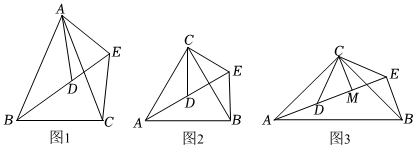
（1）問題發現：在圖1的“手拉手”圖形中，若△ABC和△ADE均是頂角為40°的等腰三角形，BC，DE分別是底邊，求證：BD=CE；
（2）拓展探究：如圖2，若△ABC和△CDE均是等邊三角形，點A，D，E在同一條直線上，連接BE，則∠AEB=6060°，線段BE與AD之間的數量關系是 BE=ADBE=AD；
（3）解決問題：如圖3，若△ABC和△DCE均是等腰直角三角形，∠ACB=∠DCE=90°，點A，D，E在同一條直線上，CM為△DCE中DE邊上的高，連接BE，請求出∠AEB的度數，寫出線段CM，AE，BE之間的數量關系，并說明理由．
【考點】三角形綜合題．
【答案】60；BE=AD
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：747引用：4難度：0.5
相似題
-
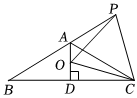1．如圖，已知△ABC中高AD恰好平分邊BC，∠B=30°，點P是BA延長線上一動點，點O是線段AD上一動點，且OP=OC，下面的結論：
①AO+AP=AB；
②OP+OC的最小值為2AB；
③∠APO+∠PCB=90°；
④S△ABC=S四邊形AOCP．
其中正確的有幾個？（ ）發布：2025/5/30 12:0:2組卷：658引用：4難度：0.3 -
2．如圖1，在△ABC中，AB=AC，BC=2，點O為△ABC兩外角∠CBD，∠BCE的平分線的交點，連接OB，OC．
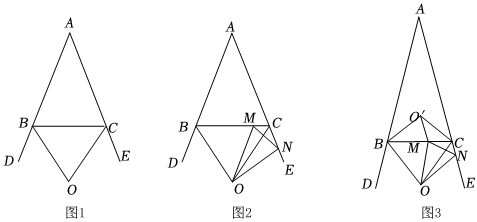
（1）求證OB=OC；
（2）如圖2，點M在線段BC上，點N為射線CE上一點，且滿足∠ABC=2∠MON．
①求△CMN的周長；
②如圖3，若∠A=30°，且點O'為∠ABC，∠ACB的平分線的交點，線段AC上是否存在一點G，使得△CGM與△CMN的周長相等？若存在，請直接寫出∠MO'G的度數；若不存在，請說明理由．發布：2025/5/30 12:0:2組卷：167引用：5難度：0.3 -
3．已知△ABC和△DEF均為等腰三角形，AB=AC，DE=DF，∠BAC=∠EDF，點E在AB上，點F在射線AC上．
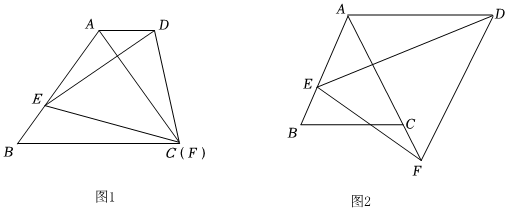
（1）如圖1，若∠BAC=60°，點F與點C重合，求證：AD∥BC；
（2）如圖2，若AD=AB，求證：AF=AE+BC．
（3）若AB=5，在（2）的條件下，點E為AB的中點，P為BC所在直線上一動點，當|DP-EP|取得最大值時，請直接寫出BP的長．發布：2025/5/30 11:30:2組卷：299引用：1難度：0.4