某數(shù)學(xué)活動(dòng)小組在一次活動(dòng)中，對(duì)一個(gè)數(shù)學(xué)問(wèn)題做了如下研究：
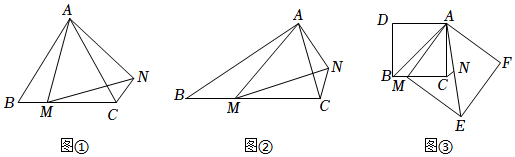
[問(wèn)題發(fā)現(xiàn)]（1）如圖①，在等邊三角形ABC中，點(diǎn)M是BC上任意一點(diǎn)，連接AM，以AM為邊作等邊三角形AMN，連接CN，則∠ABC和∠ACN的數(shù)量關(guān)系為 ∠ABC=∠ACN∠ABC=∠ACN．
[變式探究]（2）如圖②，在等腰三角形ABC中，AB=BC，點(diǎn)M是BC邊上任意一點(diǎn)（不含端點(diǎn)B，C），連接AM，以AM為邊作等腰三角形AMN，使∠AMN=∠ABC，AM=MN，連接CN，試探究∠ABC與∠ACN的數(shù)量關(guān)系，并說(shuō)明理由；
[解決問(wèn)題]（3）如圖③，在正方形ADBC中，點(diǎn)M為BC邊上一點(diǎn)，以AM為邊作正方形AMEF，點(diǎn)N為正方形AMEF的中心，連接CN，AB，AE，若正方形ADBC的邊長(zhǎng)為8，CN=2，直接寫(xiě)出正方形AMEF的邊長(zhǎng)．
2
【考點(diǎn)】四邊形綜合題．
【答案】∠ABC=∠ACN
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：736引用：5難度：0.2
相似題
-
1．如圖，四邊形ABCD中，∠A=∠B=90°，AD=2，AB=5，BC=3．
（1）如圖①，P為AB上的一個(gè)動(dòng)點(diǎn)，以PD，PC為邊作?PCQD．
①請(qǐng)問(wèn)四邊形PCQD能否成為矩形？若能，求出AP的長(zhǎng)；若不能，請(qǐng)說(shuō)明理由．
②填空：當(dāng)AP=時(shí)，四邊形PCQD為菱形；
③填空：當(dāng)AP=時(shí)，四邊形PCQD有四條對(duì)稱(chēng)軸．
（2）如圖②，若P為AB上的一點(diǎn)，以PD，PC為邊作?PCQD，請(qǐng)問(wèn)對(duì)角線PQ的長(zhǎng)是否存在最小值？若存在，請(qǐng)求出最小值；若不存在，請(qǐng)說(shuō)明理由．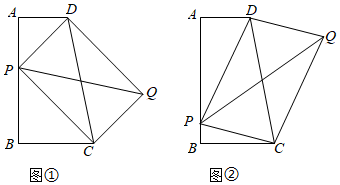
發(fā)布：2025/5/24 11:0:1組卷：701引用：3難度：0.2 -
2．綜合與實(shí)踐
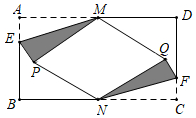
問(wèn)題情境：在數(shù)學(xué)活動(dòng)課上，老師讓同學(xué)們以“矩形的折疊”為主題開(kāi)展數(shù)學(xué)活動(dòng)如圖，矩形紙片ABCD中，點(diǎn)M、N分別是AD、BC的中點(diǎn)，點(diǎn)E、F分別在AB、CD上，且AE=CF．
動(dòng)手操作：將△AEM沿EM折疊，點(diǎn)A的對(duì)應(yīng)點(diǎn)為點(diǎn)P，將△NCF沿NF折疊，點(diǎn)C的對(duì)應(yīng)點(diǎn)為點(diǎn)Q，點(diǎn)P、Q均落在矩形ABCD的內(nèi)部，連接PN、QM．
問(wèn)題解決：（1）判斷四邊形PNQM的形狀，并證明；
（2）當(dāng)AD=2AB=4，四邊形PNQM為菱形時(shí)，求AE的長(zhǎng)．發(fā)布：2025/5/24 11:30:1組卷：112引用：2難度：0.3 -
3．（1）證明推斷：如圖（1），在正方形ABCD中，點(diǎn)E，Q分別在邊BC，AB上，DQ⊥AE于點(diǎn)O，點(diǎn)G，F(xiàn)分別在邊CD，AB上，GF⊥AE．求證：AE=FG；
（2）類(lèi)比探究：如圖（2），在矩形ABCD中，=k（k為常數(shù)）．將矩形ABCD沿GF折疊，使點(diǎn)A落在BC邊上的點(diǎn)E處，得到四邊形FEPG，EP交CD于點(diǎn)H，連接AE交GF于點(diǎn)O．試探究GF與AE之間的數(shù)量關(guān)系，并說(shuō)明理由；BCAB
（3）拓展應(yīng)用：在（2）的條件下，連接CP，當(dāng)時(shí)k=，若tan∠CGP=34，GF=243，求CP的長(zhǎng)．5
發(fā)布：2025/5/24 10:30:2組卷：3153引用：13難度：0.4