將一張長方形的紙對折，如圖所示可得到一條折痕．（圖中虛線），繼續對折，對折時每次折痕與上次的折痕保持平行，連續對折三次后，可以得7條折痕，那么對折四次可以得到1515條折痕，如果對折n次，可以得到（2n-1）（2n-1）條折痕．
【考點】規律型：圖形的變化類．
【答案】15；（2n-1）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 11:0:2組卷：962引用：67難度：0.5
相似題
-
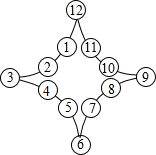1．如圖所示，圓圈內分別標有1，2，…，12，這12個數字，電子跳蚤每跳一步，可以從一個圓圈逆時針跳到相鄰的圓圈，若電子跳蚤所在圓圈的數字為n,則電子跳蚤連續跳（3n-2）步作為一次跳躍，例如：電子跳蚤從標有數字1的圓圈需跳3×1-2=1步到標有數字2的圓圈內，完成一次跳躍，第二次則要連續跳3×2-2=4步到達標有數字6的圓圈，…依此規律，若電子跳蚤從①開始，那么第3次能跳到的圓圈內所標的數字為；第2012次電子跳蚤能跳到的圓圈內所標的數字為．發布：2025/6/2 13:30:2組卷：238引用：7難度：0.5 -
2．如圖，某廣場地面的圖案是用大小相同的黑、白正方形地磚鑲嵌而成，圖中第1個黑色L形由3個正方形組成，第2個黑色L形由7個正方形組成，…那么第n個黑色L形的正方形個數是（ ）發布：2025/6/2 13:30:2組卷：324引用：11難度：0.9 -
3．如圖，均是由若干個
的基礎圖形組成的有規律的圖案，第①個圖案由4個基礎圖形組成，第②個圖案由7個基礎圖形組成…按此規律排列下去，第④個圖案中的基礎圖形個數為 ，用式子表示第n個圖案中的基礎圖形個數為 ．
發布：2025/6/2 3:0:1組卷：186引用：3難度：0.6