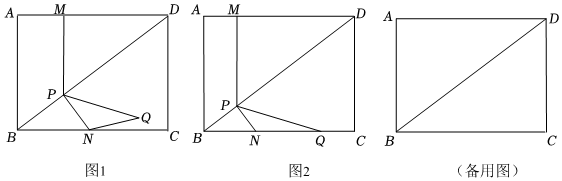
如圖1，在矩形ABCD中，AB=3，AD=4．P為對角線BD上的點，過點P作PM⊥AD于點M，PN⊥BD交BC于點N，Q是M關于PD的對稱點，連結PQ，QN．
（1）如圖2，當Q落在BC上時，求證：BQ=MD．
（2）是否存在△PNQ為等腰三角形的情況？若存在，求MP的長；若不存在，請說明理由．
（3）若射線MQ交射線DC于點F，當PQ⊥QN時，求DF：FC的值．
【考點】四邊形綜合題．
【答案】（1）見解答；（2）MP=2或或；（3）8．
5
3
25
19
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 6:0:2組卷：366引用：3難度：0.1
相似題
-
1．如圖，四邊形ABCD中，∠A=∠B=90°，AD=2，AB=5，BC=3．
（1）如圖①，P為AB上的一個動點，以PD，PC為邊作?PCQD．
①請問四邊形PCQD能否成為矩形？若能，求出AP的長；若不能，請說明理由．
②填空：當AP=時，四邊形PCQD為菱形；
③填空：當AP=時，四邊形PCQD有四條對稱軸．
（2）如圖②，若P為AB上的一點，以PD，PC為邊作?PCQD，請問對角線PQ的長是否存在最小值？若存在，請求出最小值；若不存在，請說明理由．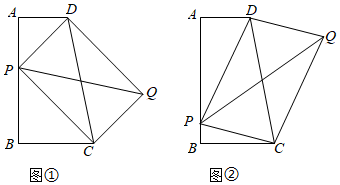
發布：2025/5/24 11:0:1組卷：701引用：3難度：0.2 -
2．（1）證明推斷：如圖（1），在正方形ABCD中，點E，Q分別在邊BC，AB上，DQ⊥AE于點O，點G，F分別在邊CD，AB上，GF⊥AE．求證：AE=FG；
（2）類比探究：如圖（2），在矩形ABCD中，=k（k為常數）．將矩形ABCD沿GF折疊，使點A落在BC邊上的點E處，得到四邊形FEPG，EP交CD于點H，連接AE交GF于點O．試探究GF與AE之間的數量關系，并說明理由；BCAB
（3）拓展應用：在（2）的條件下，連接CP，當時k=，若tan∠CGP=34，GF=243，求CP的長．5
發布：2025/5/24 10:30:2組卷：3153引用：13難度：0.4 -
3．數學學習總是循序漸進、不斷延伸拓展的，數學知識往往起源于人們為了解決某些問題，通過觀察、測量、思考、猜想出的一些結論．但是所猜想的結論不一定都是正確的．人們從已有的知識出發，經過推理、論證后，如果所猜想的結論在邏輯上沒有矛盾，就可以作為新的推理的前提，數學中稱之為定理．
（1）推理證明：
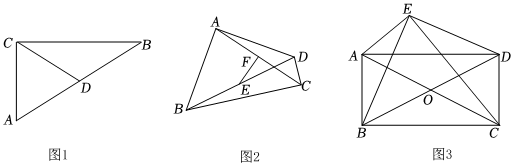
在八年級學習等腰三角形和直角三角形時，借助工具測量就能夠發現：“直角三角形斜邊上的中線等于斜邊的一半”，當時并未說明這個結論的正確性．九年級學習了矩形的判定和性質之后，就可以解決這個問題了．如圖1，在Rt△ABC中，若CD是斜邊AB上的中線，則，請你用矩形的性質證明這個結論的正確性．CD=12AB
（2）遷移運用：利用上述結論解決下列問題：
①如圖2，在線段BD異側以BD為斜邊分別構造兩個直角三角形△ABD與△CBD，E、F分別是BD、AC的中點，判斷EF與AC的位置關系并說明理由；
②如圖3，?ABCD對角線AC、BD相交于點O，分別以AC、BD為斜邊且在同側分別構造兩個直角三角形△ACE與△BDE，求證：?ABCD是矩形．發布：2025/5/24 10:30:2組卷：291引用：3難度：0.5