直線AB，CD相交于點O，OE平分∠AOD，∠FOC=70°，∠FOB=36°，求∠AOE的度數．
解：∵∠FOC=70°，∠FOB=36°，
∴∠BOC=∠FOC+∠FOBFOB=106106°．
∵直線AB，CD相交于點O，
∴∠AOD與∠BOCBOC是對頂角．
∴∠AOD=∠BOCBOC=106106°．
∵OE是∠AOD的平分線，
∴∠AOE=12∠AODAOD=5353°．
1
2
【答案】FOB；106；BOC；BOC；106；AOD；53
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 0:30:1組卷：86引用：1難度：0.8
相似題
-
1．如圖直線AB、CD相交于點E，EF是∠BED的角平分線，已知∠DEF=50°，則∠AED的度數是 ．發布：2025/6/1 17:30:1組卷：97引用：1難度：0.7 -
2．如圖，直線EF、CD相交于點O，∠AOB=90°，OC平分∠AOF．
（1）若∠AOE=40°，求∠BOD的度數；
（2）若∠AOE=30°，請直接寫出∠BOD的度數；
（3）觀察（1）、（2）的結果，猜想∠AOE和∠BOD的數量關系，并說明理由．發布：2025/6/2 9:0:1組卷：4894引用：6難度：0.3 -
3．如圖，直線AB與CD相交于點E，射線EG在∠AEC內（如圖1）．
（1）若∠BEC的補角是它的余角的3倍，則∠BEC=°；
（2）在（1）的條件下，若∠CEG比∠AEG小25度，求∠AEG的大小；
（3）若射線EF平分∠AED，∠FEG=m°（m＞90°）（如圖2），則∠AEG-∠CEG=°（用m的代數式表示）．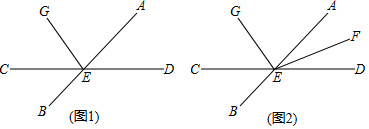
發布：2025/6/2 11:30:1組卷：663引用：4難度：0.7