閱讀下面材料，完成（1）～（3）題．
數學課上，老師出示了這樣一道題：
如圖1，△ABC中，AC=BC=a,∠ACB=90°，點D在AB上，且AD=kAB（其中0＜k＜12），直線CD繞點D順時針旋轉90°與直線CB繞點B逆時針旋轉90°后相交于點E，探究線段DC、DE的數量關系，并證明．
同學們經過思考后，交流了自己的想法：
小明：“通過觀察和度量，發現DC與DE相等”；
小偉：“通過構造全等三角形，經過進一步推理，可以得到DC與DE相等”
小強：“通過進一步的推理計算，可以得到BE與BC的數量關系”
老師：“保留原題條件，連接CE交AB于點O．如果給出BO與DO的數量關系，那么可以求出CO?EO的值”
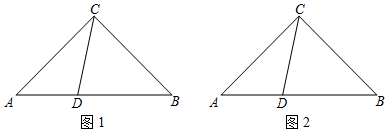
（1）在圖1中將圖補充完整，并證明DC=DE；
（2）直接寫出線段BE與BC的數量關系BE=（1-2k）BCBE=（1-2k）BC（用含k的代數式表示）；
（3）在圖2中將圖補充完整，若BO=513DO，求CO?EO的值（用含a的代數式表示）．
1
2
5
13
【考點】幾何變換綜合題．
【答案】BE=（1-2k）BC
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：538引用：2難度：0.2
相似題
-
1．如圖，在Rt△ABC中，點P為斜邊BC上一動點，將△ABP沿直線AP折疊，使得點B的對應點為B'，連接CB'，BB'．
（1）如圖1，若PB=AB，求證：PB'⊥AC．
（2）如圖2，若AB=AC，BP=3PC，求tan∠CPB'的值．
（3）如圖3，若∠ACB=30°，且AB=CB'，請直接寫出此時的值．PCAB
發布：2025/6/9 21:30:1組卷：233引用：2難度：0.2 -
2．在Rt△ABC中，∠ACB=90°，AC=3，BC=4．將Rt△ABC繞點B順時針旋轉α（0°＜α＜60°）得到Rt△DEB，直線DE，AC交于點P．
（1）如圖1，當BD⊥BC時，連接BP．
①求△BDP的面積；
②求tan∠CBP的值；
（2）如圖2，連接AD，若F為AD中點，求證：C，E，F三點共線．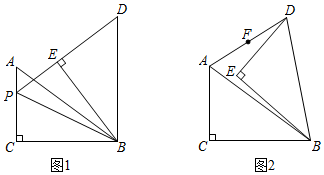
發布：2025/6/9 17:0:1組卷：511引用：4難度：0.1 -
3．在△ABC中，∠BAC=90°，AB=AC，線段AB繞點A逆時針旋轉至AD（AD不與AC重合），旋轉角記為α，∠DAC的平分線AE與射線BD相交于點E，連接EC．
（1）如圖①，當α=20°時，∠AEB的度數是 ；
（2）如圖②，當0°＜α＜90°時，求證：；BD+2CE=2AE
（3）當0°＜α＜180°，AE=2CE時，請直接寫出tan∠BCE的值．發布：2025/6/9 20:30:1組卷：312引用：3難度：0.1