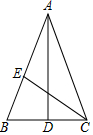
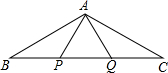
如圖，AQ∥BP，AB⊥BP，E、C、D分別是線段AQ、AB、BP上的點，且滿足EC⊥CD．EF是∠GEC的角平分線與BP交于點F，在EQ上截一點G，連接GF，令GF=FE．
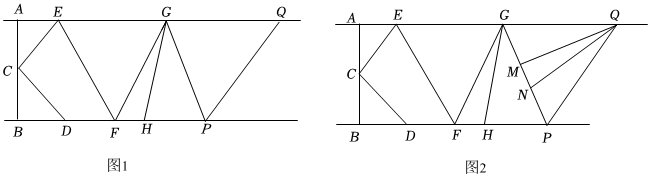（1）如圖1，若∠AEC=40°，求∠CDB的度數(shù)．
（2）如圖1，連接GP，若GP∥EF，H是線段FP上的一點（FH＜HP），連接GH，使得2∠GHP=3∠AEC，求∠FGH和∠CDB的數(shù)量關(guān)系．
（3）如圖2，在（2）的條件下，過點Q作QM⊥GP，垂足為M．N是線段GP上的一點，且滿足∠QNM=32∠GEF．求∠GQN和∠CEF的數(shù)量關(guān)系．
3
2
【考點】等腰三角形的性質(zhì)；平行線的性質(zhì)．
【答案】（1）∠CDB=50°；
（2）∠CDB+2∠FGH=90°；
（3）∠GQN+2.5∠CEF=180°．
（2）∠CDB+2∠FGH=90°；
（3）∠GQN+2.5∠CEF=180°．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/16 8:0:9組卷：270引用：1難度：0.4
