【綜合與實踐】現(xiàn)實生活中,人們可以借助光源來測量物體的高度.已知榕樹CD,F(xiàn)G和燈柱AB如圖①所示,在燈柱AB上有一盞路燈P,榕樹和燈柱的底端在同一水平線上,兩棵榕樹在路燈下都有影子,只要測量出其中一些數(shù)據(jù),則可求出所需要的數(shù)據(jù),具體操作步驟如下:
①根據(jù)光源確定榕樹在地面上的影子;
②測量出相關數(shù)據(jù),如高度,影長等;
③利用相似三角形的相關知識,可求出所需要的數(shù)據(jù).
根據(jù)上述內(nèi)容,解答下列問題:
(1)已知榕樹CD在路燈下的影子為DE,請畫出榕樹FG在路燈下的影子GH;
(2)如圖①,若榕樹CD的高度為3.6米,其離路燈的距離BD為6米,兩棵榕樹的影長DE,GH均為4米,兩棵樹之間的距離DG為6米,求榕樹FG的高度;
(3)無論太陽光還是點光源,其本質與視線問題相同.日常生活中我們也可以直接利用視線解決問題.如圖②,建筑物CD高為50米,建筑物MF上有一個廣告牌EM,合計總高度EF為70米,兩座建筑物之間的直線距離FD為30米.一個觀測者(身高不計)先站在A處觀測,發(fā)現(xiàn)能看見廣告牌EM的底端M處,觀測者沿著直線AF向前走了5米到B處觀測,發(fā)現(xiàn)剛好看到廣告牌EM的頂端E處.則廣告牌EM的高度為 5454米.
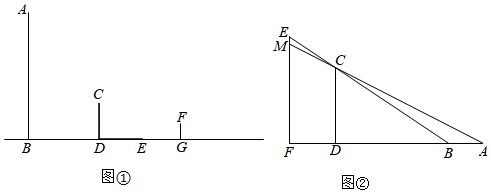
5
4
5
4
【考點】相似形綜合題.
【答案】
5
4
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/9/13 7:0:8組卷:1522引用:3難度:0.3
相似題
-
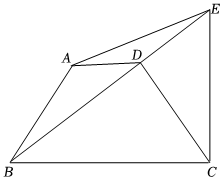 1.在四邊形ABCD中,AD∥BC,AB=CD,對角線BD⊥CD,過點C作CE⊥BC交BD的延長線于點E,連接AE.
1.在四邊形ABCD中,AD∥BC,AB=CD,對角線BD⊥CD,過點C作CE⊥BC交BD的延長線于點E,連接AE.
(1)證明:△CED∽△BEC;
(2)若EC=EA,證明:=EDAD;ECCD
(3)在(2)的條件下,試求tan∠EAD的值.發(fā)布:2025/5/24 16:30:1組卷:205引用:3難度:0.3 -
2.如圖1,在△ABC中,∠BAC=90°,AB=6.AC=8,點D,E分別是AB,BC的中點.把△BDE繞點B旋轉一定角度,連結AD,AE,CD,CE.
(1)如圖2,當線段BD在△ABC內(nèi)部時,求證:△BAD∽△BCE.
(2)當點D落在直線AE上時,請畫出圖形,并求CE的長.
(3)當△ABE面積最大時,請畫出圖形,并求出此時△ADE的面積.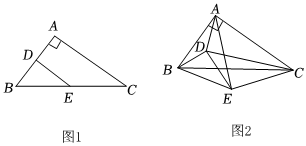 發(fā)布:2025/5/24 17:0:2組卷:185引用:1難度:0.4
發(fā)布:2025/5/24 17:0:2組卷:185引用:1難度:0.4 -
3.在平行四邊形ABCD中,AD=8,DC=6,∠FED的頂點在BC上,EF交直線AB于F點.
(1)如圖1,若∠FED=∠B=90°,BE=5,求BF的長;
(2)如圖2,在AB上取點G,使BG=BE,連接EG,若∠B=∠FED=60°,求證:;EFED=BECD
(3)如圖3,若∠ABC=90°,點C關于BD的對稱點為點C',CC′交BD于點M,對角線AC、BD交于點O,連接OC'交AD于點G,求AG的長.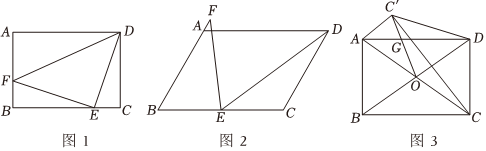 發(fā)布:2025/5/24 14:30:1組卷:496引用:4難度:0.1
發(fā)布:2025/5/24 14:30:1組卷:496引用:4難度:0.1


