閱讀材料：若m2-4m+n2+6n+13=0，求m,n的值．
解：∵m2-4m+n2+6n+13=0∴（m2-4m+4）+（n2+6n+9）=0∴（m-2）2+（n+3）2=0∵（m-2）2≥0，（n+3）2≥0∴m-2=0，n+3=0∴m=2，n=-3．
根據你的觀察，解答下列問題：
（1）已知△ABC的三邊長分別為a,b,c,且a2+b2-12a-16b+c-10+100=0，則△ABC為直角直角三角形；
（2）已知x2-4xy+5y2+y+14=0，求x和y的值；
（3）證明：無論x,y取何值多項式x2+y2-2x-2y+6的值總是正數．
c
-
10
1
4
【考點】配方法的應用；非負數的性質：偶次方．
【答案】直角
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：151引用：1難度：0.5
相似題
-
1．閱讀下列材料：
利用完全平方公式，將多項式x2+bx+c變形為（x+m）2+n的形式，然后由（x+m）2≥0就可求出多項式x2+bx+c的最小值．
例題：求x2-12x+37的最小值：
解：x2-12x+37=x2-2x?6+62-62+37=（x-6）2+1
因為不論x取何值，（x-6）2總是非負數，即（x-6）2≥0．
所以（x-6）2+1≥1．
所以當x=6時，x2-12x+37有最小值，最小值是1．
根據上述材料，解答下列問題：
（1）填空：x2-8x+=（x-）2；
（2）將x2+10x-2變形為（x+m）2+n的形式，并求出x2+10x-2的最小值；
（3）如圖所示的第一個長方形邊長分別是2a+5、3a+2，面積為S1；如圖所示的第二個長方形邊長分別是5a、a+5，面積為S2；試比較S1與S2的大小，并說明理由．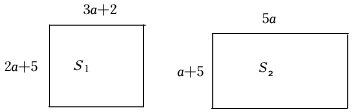
發布：2025/6/7 8:30:2組卷：174引用：1難度：0.4 -
2．對于二次三項式x2+6x+3，若x取值為m,則二次三項式的最小值為n,那么m+n的值為 ．
發布：2025/6/7 7:30:1組卷：73引用：2難度：0.7 -
3．閱讀理解：我們一起來探究代數式x2-4x-5的值，
探究一：當x=1時，x2-4x-5的值為 ；當x=-3時，x2-4x-5的值為 ，可見，代數式的值因x的取值不同而變化．
探究二：把代數式x2-4x-5進行變形，如：x2-4x-5=x2-4x+4-9=（x-2）2-9，可以看出代數式x2-4x-5的最小值為 ，這時相應的x=．
根據上述探究，請解答：
（1）求代數式-x2-8x+17的最大值，并寫出相應x的值．
（2）把（1）中代數式記為A，代數式9y2+12y+37記為B，是否存在，x,y的值，使得A與B的值相等？若能，請求出此時x?y的值，若不能，請說明理由．發布：2025/6/7 1:30:1組卷：287引用：3難度：0.5