代數(shù)式求值：
（1）已知2x-y=13，xy=2，求2x4y3-x3y4的值；
（2）已知a+b=2，求（a2-b2）2-8（a2+b2）的值．
2
x
-
y
=
1
3
，
xy
=
2
【考點】因式分解的應用．
【答案】（1）1；（2）-16．
3
5
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/9/13 6:0:10組卷：187引用：2難度：0.5
相似題
-
1．設a、b為任意不相等的正數(shù)，且
，x=b2+4a，則x、y一定（ ）y=a2+4b發(fā)布：2025/5/25 18:30:1組卷：50引用：1難度：0.6 -
2．一個四位正整數(shù)P滿足千位上的數(shù)字比百位上的數(shù)字大2，十位上的數(shù)字比個位上的數(shù)字大2，千位上的數(shù)字與十位上的數(shù)字不相等且各個數(shù)位上的數(shù)字均不為零，則稱P為“雙減數(shù)”，將“雙減數(shù)”P的千位和十位數(shù)字組成的兩位數(shù)與百位和個位數(shù)字組成的兩位數(shù)的和記為M（P），將“雙減數(shù)”P的千位和百位數(shù)字組成的兩位數(shù)與十位和個位數(shù)字組成的兩位數(shù)的差記為N（P），并規(guī)定F（P）=
．M（P）N（P）
例如：四位正整數(shù)7564，∵7-5=6-4=2，且7≠6，∴7564是“雙減數(shù)”，此M（7564）=76+54=130，N（7564）=75-64=11，∴F（7564）=．13011
（1）填空：F（3186）=，并證明對于任意“雙減數(shù)”A，N（A）都能被11整除；
（2）若“雙減數(shù)”P為偶數(shù)，且M（P）-N（P）能被6整除，求滿足條件的所有“雙減數(shù)”P，并求F（P）的值．發(fā)布：2025/5/25 17:0:1組卷：383引用：2難度：0.5 -
3．【實踐操作】
小明在學習了八下數(shù)學課本中“因式分解”章節(jié)，用各若立體方塊進行實踐操作探究，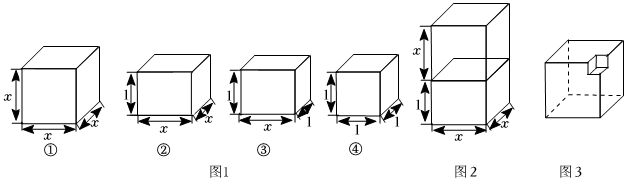
【溫故知新】
如圖，現(xiàn)有編號為①②③④的四種長方體各若干塊，現(xiàn)取其中兩塊拼成一個大長方體如圖2，據(jù)此寫出一個多項式的因式分解：．
【問題解決】
如圖，若要用這四種長方體拼成一個棱長為（x+1）的正方體，需要②號長方體 個，③號長方體 個，據(jù)此寫出一個多項式的因式分解：．
【拓展與延伸】
如圖3，在一個棱長為a的正方體中挖出一個棱長為b的正方體，據(jù)此寫出a3-b3=．發(fā)布：2025/5/25 16:0:2組卷：217引用：2難度：0.4
相關(guān)試卷