我們定義：如果一個矩形A周長和面積都是B矩形的N倍，那么我們就稱矩形A是矩形B的完全N倍體．
?
（1）若矩形A為正方形，是否存在一個正方形B是正方形A的完全2倍體？不存在不存在（填“存在”或“不存在”）．
【深入探究】長為3，寬為2的矩形C是否存在完全2倍體？
小鳴和小棋分別有以下思路：
【小鳴方程流】設(shè)新矩形長和寬為x、y,則依題意x+y=10，xy=12，聯(lián)立x+y=10 xy=12
，得x2-10x+12=0，再探究根的情況；
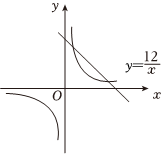
【小棋函數(shù)流】如圖，也可用反比例函數(shù)l2：y=12x與一次函數(shù)l1：y=-x+10來研究，作出圖象，有交點(diǎn)，意味著存在完全2倍體．
（2）那么長為4．寬為3的矩形C是否存在完全12倍體？請利用上述其中一種思路說明原因；
（3）如果長為4，寬為3的矩形C存在完全k倍體，請求出k的取值范圍．
x + y = 10 |
xy = 12 |
y
=
12
x
1
2
【考點(diǎn)】反比例函數(shù)綜合題．
【答案】不存在
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/5 8:0:9組卷：775引用：2難度：0.6
相似題
-
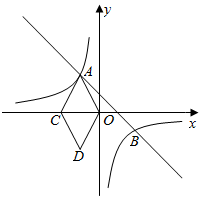1．如圖，一次函數(shù)y=mx+1的圖象與反比例函數(shù)y=的圖象相交于A、B兩點(diǎn)，點(diǎn)C在x軸負(fù)半軸上，點(diǎn)D（-1，-2），連接OA、OD、DC、AC，四邊形OACD為菱形．kx
（1）求一次函數(shù)與反比例函數(shù)的解析式；
（2）根據(jù)圖象，直接寫出反比例函數(shù)的值小于2時，x的取值范圍；
（3）設(shè)點(diǎn)P是直線AB上一動點(diǎn)，且S△OAP=S菱形OACD，求點(diǎn)P的坐標(biāo)．12發(fā)布：2025/5/25 4:30:1組卷：1258引用：5難度：0.5 -
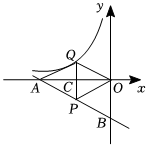2．如圖，一次函數(shù)的圖象分別交x軸，y軸于A，B兩點(diǎn)，P為AB的中點(diǎn)，PC⊥x軸于點(diǎn)C，延長PC交反比例函數(shù)y=-12x-2（k＜0）的圖象于點(diǎn)Q，且y=kx．tan∠AOQ=12
（1）求k的值；
（2）連接OP、AQ，求證：四邊形APOQ是菱形．發(fā)布：2025/5/25 4:30:1組卷：11引用：3難度：0.2 -
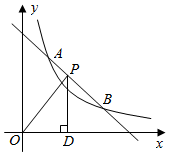3．如圖，一次函數(shù)y1=-x+4與反比例函數(shù)y2=（x＞0）的圖象交于A，B兩點(diǎn)．3x
（1）求點(diǎn)A，點(diǎn)B的坐標(biāo)：
（2）點(diǎn)P是直線AB上一點(diǎn)，設(shè)點(diǎn)P的橫坐標(biāo)為m.填空：
①當(dāng)y1＜y2時，m的取值范圍是；
②點(diǎn)P在線段AB上，過點(diǎn)P作PD⊥x軸于點(diǎn)D，連接OP．若△POD的面積最小時，則m的值為．發(fā)布：2025/5/25 5:30:2組卷：510引用：10難度：0.6