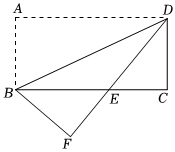
如圖，將矩形紙片ABCD沿對角線BD折疊，使點A落在平面上的F點處，DF交BC于點E．
（1）求證：△DCE≌△BFE；
（2）若CD=2，∠ADB=30°，求BE的長．
【考點】翻折變換（折疊問題）；全等三角形的判定與性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：3576引用：66難度：0.7
相似題
-
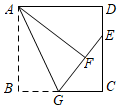1．如圖，正方形紙片ABCD中，AB=6，G是BC的中點．將△ABG沿AG翻折至△AFG，延長GF交DC于點E，則DE的長等于．發布：2025/5/26 11:0:2組卷：671引用：5難度：0.7 -
2．如圖，在△ABC紙片中，∠ABC=90°，將其折疊，使得點C與點A重合，折痕為DE，若AB=3cm,AC=5cm,則△ABE的周長為（ ）發布：2025/5/26 11:0:2組卷：46引用：2難度：0.5 -
3．如圖，矩形ABCD中，E是CD邊上一點，沿AE折疊△ADE，使點D恰好落在BC邊上的點F處，作FG⊥BC交AE于點G，若AD=10，AB=8，則FG的長為（ ）發布：2025/5/26 10:30:2組卷：117引用：5難度：0.4