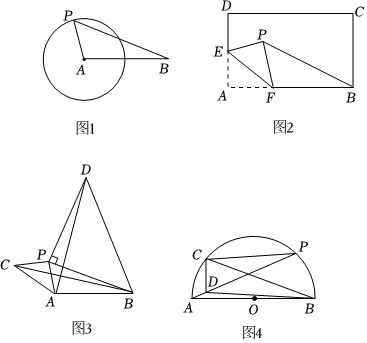
（1）發現，如圖1，在平面內，已知⊙A的半徑為r,B為⊙A外一點，且AB=a.P為⊙A上一動點，連接PA，PB，易得PB的最大值為 a+ra+r，最小值為 a-ra-r．（用含a、r的代數式表示）
（2）應用，①如圖2，在矩形ABCD中，AB=6，BC=4，E為AD中點，F為AB邊上一動點，在平面內沿EF將△AEF翻折得到△PFF，連接PB，則PB的最小值為 210-2210-2．
②如圖3，P為線段AB外一動點，分別以PA，PB為直角邊，P為直角頂點，作等腰Rt△APC和等腰Rt△BPD，連接BC、AD．若AP=42，AB=9，求AD的最大值．
（3）拓展：如圖4，已知以AB為直徑的半圓O，C為弧AB上一點，∠ABC=30°，P為弧BC上任意一點，CD⊥CP交AP于D，連接BD，若AB=6，則BD的最小值為 57-357-3．
10
-
2
10
-
2
2
57
-
3
57
-
3
【考點】圓的綜合題．
【答案】a+r；a-r；2；
10
-
2
57
-
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/4 16:0:8組卷：261引用：2難度：0.2
相似題
-
1．在⊙O中，直徑AB與弦CD（非直徑）交于點E，DE=CE，弦BG⊥BC交⊙O于點G，交CD于點F．
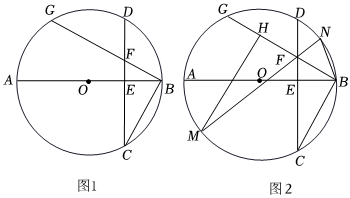
（1）如圖1，求證：∠ABF=∠BCD；
（2）如圖2，點N為弧BD上一點，連接BN、NF，并延長NF交⊙O于點M，H為FG上一點，連接MH，BN=BF，∠HMF=∠HBN，求證：FH=GH．12發布：2025/5/24 14:30:1組卷：107引用：1難度：0.1 -
2．已知在Rt△ABC中，∠C=90°，AC=
，BC=2．23
（1）如圖①，若P為BC上由點B向點C運動的一點，連接AP，設AP的中點為G，求在點P運動的過程中，點G經過的路徑長．
（2）如圖②，若P是以AB為直徑所作半圓上由點A沿著半圓向點B運動的一點，求CP的中點F經過的路徑長．
（3）如圖③，若P為BC上由點B向點C運動的一點，連接AP，作BR⊥AP于點R，（P、R可以重合）求在點P的運動過程中，R經過的路徑長．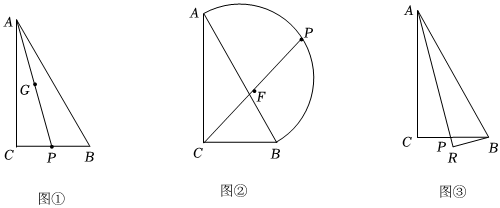
發布：2025/5/24 13:30:2組卷：86引用：1難度：0.3 -
3．如圖1，在Rt△ABC中，∠ABC=90°，以線段BC為直徑作⊙O交AC于點D，E為AB中點，連接ED，過點C作CF∥AB交ED的延長線于點F．
（1）求證：直線ED是⊙O的切線；
（2）判斷△CDF的形狀，并說明理由；
（3）如圖2，連接OF交⊙O于點P，連接BP交AC于點Q，若D為AQ中點，AB=6，求PQ的長．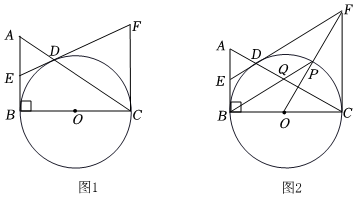
發布：2025/5/24 13:30:2組卷：319引用：2難度：0.3