當(dāng)前位置：新人教版七年級(jí)上冊《第1章有理數(shù)》2020年單元測試卷（13）> 試題詳情

觀察下列等式：
1
1
×
2
=1-
1
2
；
1
2
×
3
=
1
2
-
1
3
；
1
3
×
4
=
1
3
-
1
4
；…；
1
n
（
n
+
1
）
=
1
n
-
1
n
+
1
．
將以上幾個(gè)式子相加得到：
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+…+
1
n
（
n
+
1
）
=1-
1
n
（
n
+
1
）
；
用上述方法計(jì)算下面式子的結(jié)果：
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+…+
1
99
×
101
．

【考點(diǎn)】規(guī)律型：數(shù)字的變化類．

【答案】

101

．

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

發(fā)布：2024/4/20 14:35:0組卷：52引用：2難度：0.6

相似題

1．觀察下列等式：
第1個(gè)等式：
（
1
-
1
3
）
÷
4
3
=
1
2
；
第2個(gè)等式：
（
1
-
1
4
）
÷
9
8
=
2
3
；
第3個(gè)等式：
（
1
-
1
5
）
÷
16
15
=
3
4
；
第4個(gè)等式：
（
1
-
1
6
）
÷
25
24
=
4
5
；
第5個(gè)等式：
（
1
-
1
7
）
÷
36
35
=
5
6
；
……
按照以上規(guī)律，解決下列問題：
（1）寫出第6個(gè)等式：
；
（2）寫出你猜想的第n個(gè)等式
（用含n的等式表示），并證明．
發(fā)布：2025/5/25 18:30:1組卷：100引用：3難度：0.7
解析
2．設(shè)
f
（
x
）
=
a
1
x
+
a
2
x
2
+
…
+
a
n
x
n
（n為正整數(shù)），若f（1）=n²，則（　　）
A．a(chǎn)_n=2n-1，
f
（
1
3
）
的最小值為1
B．a(chǎn)_n=n,
f
（
1
3
）
的最小值為
1
3
C．a(chǎn)_n=2n-1，
f
（
1
3
）
的最小值為
1
3
D．a(chǎn)_n=n,
f
（
1
3
）
的最小值為
2
3
發(fā)布：2025/5/25 19:30:2組卷：186引用：1難度：0.3
解析
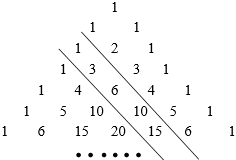3．如圖，被稱為“楊輝三角”或“賈憲三角”．其規(guī)律是：從第二行起，每行兩端的數(shù)都是“1”，其余各數(shù)都等于該數(shù)“兩肩”上的數(shù)之和，表中兩平行線之間的一列數(shù)：1，3，6，10，15，…，我們把第一個(gè)數(shù)記為a₁，第二個(gè)數(shù)記為a₂，第三個(gè)數(shù)記為a₃，…，第n個(gè)數(shù)記為a_n．則a₁₀₀的值為（　　）
A．100 B．199 C．5050 D．10000
發(fā)布：2025/5/25 17:30:1組卷：333引用：3難度：0.7
解析

相關(guān)試卷

新人教版七年級(jí)上冊《第1章有理數(shù)》2020年單元測試卷（13）

觀察下列等式：11×2=1-12；12×3=12-13；13×4=13-14；…；1n（n+1）=1n-1n+1．將以上幾個(gè)式子相加得到：11×2+12×3+13×4+…+1n（n+1）=1-1n（n+1）；用上述方法計(jì)算下面式子的結(jié)果：11×3+13×5+15×7+…+199×101．

2．設(shè)f（x）=a1x+a2x2+…+anxn（n為正整數(shù)），若f（1）=n2，則（ ）

2．設(shè)
f
（
x
）
=
a
1
x
+
a
2
x
2
+
…
+
a
n
x
n
（n為正整數(shù)），若f（1）=n²，則（　　）