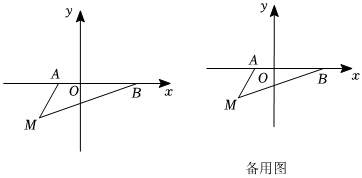
如圖，在平面直角坐標系中，已知A（a,0），B（b,0），其中a,b滿足（a+1）2+|3a+b|=0．
（1）填空：a=-1-1，b=33；
（2）若存在點M（-2，m）（m＜0），點M到x軸距離 -m-m，△ABM的面積 22．（用含m的式子表示）
（3）在（2）的條件下，當m=-1.5時，在y軸上有一點P，使得△MOP的面積與△ABM的面積相等，求出點P的坐標．
?
【考點】三角形綜合題．
【答案】-1；3；-m；2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/4 3:30:2組卷：127引用：1難度：0.4
相似題
-
1．將兩塊直角三角板（即兩個直角三角形，其中∠C=30°，∠CDO=60°；∠OAB=∠OBA=45°） 的直角頂點O按圖1方式疊放在一起，△COD繞著點O順時針旋轉一周，旋轉的速度為每秒10°，若旋轉時間為t秒，請回答下列問題：
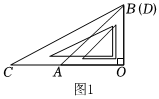
（1）當t=9時，直線OD與OB的位置關系是 ；當0＜t＜9時，（如圖2及其簡化圖），∠BOC的度數為 （用含t的代數式表示）．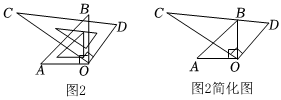
（2）當邊OB∥CD時，t的值是 ．
（3）當邊AB∥CD時，求t的值．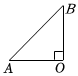
發布：2025/6/6 1:30:1組卷：109引用：1難度：0.2 -
2．先閱讀下面一段文字，再回答問題：
已知在平面直角坐標系xOy中，對于任意兩點P1（x1，y1）與P2（x2，y2）的“識別距離”，給出如下定義：若|x1-x2|＞|y1-y2|，則點P1（x1，y1）與P2（x2，y2）的“識別距離”為|x1-x2|；若|x1-x2|＜|y1-y2|，則點P1（x1，y1）與P2（x2，y2）的“識別距離”為|y1-y2|；
（1）已知點A（-1，0），B為y軸上的動點．
①若點A與點B的“識別距離”為3，寫出滿足條件的點B的坐標；
②直接寫出點A與點B的“識別距離”的最小值．
（2）已知點，D（1，1），求點C與點D的“識別距離”的最小值及相應的點C的坐標．C（m,34m+3）發布：2025/6/6 1:30:1組卷：241引用：1難度：0.1 -
3．如圖1，在平面直角坐標系中，A（a,0），C（b,4），且滿足（a+5）2+
=0，過C作CB⊥x軸于B．b-5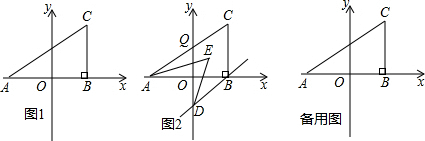
（1）a=，b=，三角形ABC的面積=；
（2）若過B作BD∥AC交y軸于D，且AE，DE分別平分∠CAB，∠ODB，如圖2，求∠AED的度數；
（3）在y軸上是否存在點P，使得三角形ABC和三角形ACP的面積相等？若存在，求出P點坐標；若不存在，請說明理由．發布：2025/6/6 0:30:1組卷：1009引用：5難度：0.1