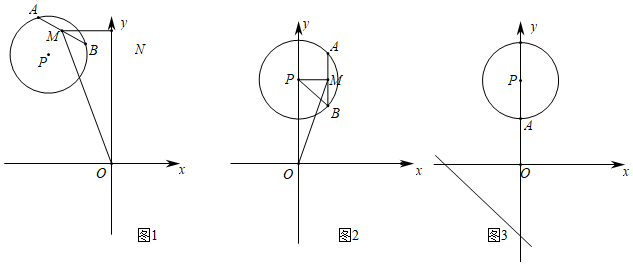
【閱讀材料】如圖1所示，對于平面內⊙P，在⊙P上有弦AB，取弦AB的中點M，我們把弦AB的中點M到某點或某直線的距離叫做弦AB到這點或者這條直線的“密距”．例如：圖1中線段MO的長度即為弦AB到原點O的“密距”，過點M作y軸的垂線交y軸于點N，線段MN的長度即為弦AB到y軸的“密距”．
【類比應用】已知⊙P的圓心為P（0，8），半徑為4，弦AB的長度為4，弦AB的中點為M．
（1）當AB∥y軸時，如圖2所示，圓心P到弦AB的中點M的距離是 2323，此時弦AB到原點O的“密距”是 219219．
（2）①如果弦AB在⊙P上運動，在運動過程中，圓心P到弦AB的中點M的距離變化嗎？若不變化，請求出PM的長，若變化，請說明理由．
②直接寫出弦AB到原點的“密距”d的取值范圍 8-23≤d≤8+238-23≤d≤8+23；
【拓展應用】如圖3所示，已知⊙P的圓心為P（0，8），半徑為4，點A（0，4），點B為⊙P上的一動點，弦AB到直線y=-x-6的“密距”的最大值是 62+262+2（直接寫出答案）．
3
3
19
19
3
3
3
3
2
2
【考點】圓的綜合題．
【答案】2；2；8-2≤d≤8+2；6+2
3
19
3
3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：198引用：3難度：0.2
相似題
-
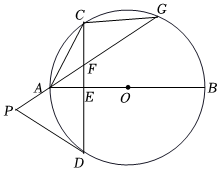1．如圖，AB為⊙O的直徑，弦CD⊥AB于點E，F是CD上一點，且AF=CF，點P在FA的延長線上，且∠PFD=∠PDF，延長PF與⊙O交于點G，連接AC，CG．
（1）求證：△AFC∽△ACG；
（2）求證：PD是⊙O的切線；
（3）若tanG=，BE-AE=34，求73的值．S△AFCS△CFG發布：2025/5/24 5:30:2組卷：72引用：1難度：0.4 -
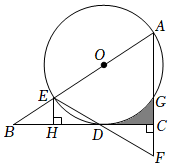2．如圖，在△AEF中，∠F=∠AEF，以AE為直徑作⊙O，分別交邊AF和邊EF于點G和點D，過點D作DC⊥AF交AF于點C，延長CD交AE的延長線于點B，過點E作EH⊥BC于點H．
（1）試判斷BD與⊙O的位置關系，并說明理由；
（2）證明：EH=CF．
（3）若∠B=30°，AE=12，求圖中陰影部分的面積．發布：2025/5/24 6:0:2組卷：164引用：5難度：0.2 -
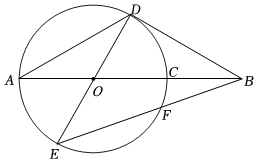3．如圖，線段AB經過⊙O的圓心O，交⊙O于A，C兩點，AD為⊙O的弦，連接BD，∠A=∠ABD=30°，連接DO并延長，交⊙O于點E，連接BE交⊙O于點F．
（1）求證：BD是⊙O的切線；
（2）求證：2AD2=DE?AB；
（3）若BC=1，求BF的長．發布：2025/5/24 6:30:2組卷：547引用：3難度：0.7