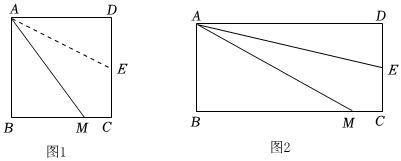
如圖1，四邊形ABCD是正方形，M是BC邊上的一點(diǎn)，E是CD邊的中點(diǎn)，AE對(duì)折后與∠MAE沿著AE對(duì)折后與∠MAE重合．
（1）證明：AM=AD+MC；
（2）AM=DE+BM是否成立？若成立，請(qǐng)給出證明，若不成立，請(qǐng)說(shuō)明理由．
（3）若四邊形ABCD是長(zhǎng)與寬不相等的矩形，其他條件不變，如圖2所示，（1）、（2）中的結(jié)論是否成立？請(qǐng)分別作出判斷，不需要證明．
【考點(diǎn)】四邊形綜合題．
【答案】（1）證明見解析；
（2）AM=DE+BM成立，理由見解析；
（3）（1）結(jié)論AM=AD+MC仍然成立，理由見解析；
（2）結(jié)論AM=DE+BM不成立．理由見解析．
（2）AM=DE+BM成立，理由見解析；
（3）（1）結(jié)論AM=AD+MC仍然成立，理由見解析；
（2）結(jié)論AM=DE+BM不成立．理由見解析．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：24引用：1難度：0.5
相似題
-
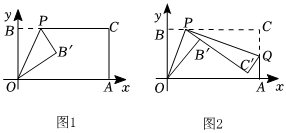1．已知一個(gè)矩形紙片OACB，將該紙片放置在平面直角坐標(biāo)系中，點(diǎn)A（11，0），點(diǎn)B（0，6），點(diǎn)P為BC邊上的動(dòng)點(diǎn)（點(diǎn)P不與點(diǎn)B、C重合）．經(jīng)過點(diǎn)O，P折疊該紙片，得點(diǎn)B'和折痕OP．設(shè)BP=t.
（1）如圖1，當(dāng)∠BOP=30°時(shí)，求點(diǎn)P的坐標(biāo)；
（2）如圖2，經(jīng)過點(diǎn)P再次折疊紙片，使點(diǎn)C落在直線PB'上，得點(diǎn)C'和折痕PQ，若AQ=m,試用含有t的式子表示m；
（3）在（2）的條件下，當(dāng)點(diǎn)C'恰好落在邊OA上時(shí)，求點(diǎn)P的坐標(biāo)．發(fā)布：2025/5/24 14:0:2組卷：275引用：1難度：0.4 -
2．[問題提出]
（1）如圖①，AB為半圓的直徑，O為圓心，C，D為半圓上的兩點(diǎn)，若OB=5，BC=6，則sin∠BDC=．
[問題探究]
（2）如圖②，在矩形ABCD中，AB=8，BC=10，點(diǎn)P在直線AB的右側(cè)，且滿足tan∠APB=2，求點(diǎn)P到CD的最短距離．
[問題解決]
（3）如圖③，有一塊矩形ABCD型板材，AB=4米，AD=6米，由于工作需要，工人王師傅想在這塊板材上找一點(diǎn)P，裁出△ABP與△ADP，并滿足cos∠APB=，S△ADP：S△ABP=3：2．請(qǐng)問王師傅的設(shè)想可以實(shí)現(xiàn)嗎？如果可以，請(qǐng)幫他計(jì)算所裁得的△ABP的面積；如果不能，請(qǐng)說(shuō)明你的理由．35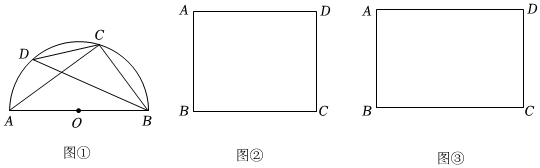
發(fā)布：2025/5/24 14:0:2組卷：959引用：3難度：0.1 -
3．如圖，在四邊形OABC中，OA=OC，∠OAB=∠OCB=90°，∠AOC=120°．過點(diǎn)O作∠DOE=60°，兩邊OD，OE分別與邊BC，AB所在直線相交于點(diǎn)D，E，連接DE．
（1）AB與BC的數(shù)量關(guān)系是 ．
（2）如圖1，當(dāng)點(diǎn)D，E分別在邊BC，AB上時(shí)，可得出結(jié)論AE+CD=DE，請(qǐng)證明這個(gè)結(jié)論．（提示：將△AOE繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)120°）
（3）如圖2，當(dāng)點(diǎn)D，E分別在邊BC，AB的延長(zhǎng)線上時(shí)，（2）中的結(jié)論還成立嗎？若成立，請(qǐng)說(shuō)明理由；若不成立，請(qǐng)直接寫出線段AE，CD，DE之間的數(shù)量關(guān)系．
發(fā)布：2025/5/24 14:0:2組卷：180引用：5難度：0.1