（1）發現問題
如圖1，△ACB和△DCE均為等邊三角形，當△DCE旋轉至點A，D，E在同一直線上，連接BE．
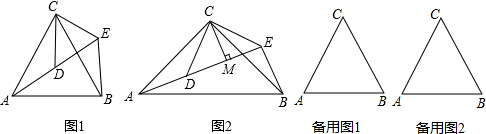
填空：
①∠AEB的度數為 60°60°；
②線段AD，BE之間的數量關系為 AD=BEAD=BE．
（2）拓展研究
如圖2，△ACB和△DCE均為等腰三角形，∠ACB=∠DCE=90°，點A，D，E三點在同一直線上，CM為△DCE中DE邊上的高，連接BE，請判斷∠AEB的度數及線段CM，AE，BE之前的數量關系，并說明理由．
（3）探究發現
圖1中的△ACB和△DCE，在△DCE旋轉中當點A，D，E在不同一直線上時，設AD與BE相交于點O，旋轉角θ（0°＜θ＜180°）嘗試在圖3中探索∠AOE的度數，直接寫出結果，不必說明理由．
【考點】幾何變換綜合題．
【答案】60°；AD=BE
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1828引用：4難度：0.5
相似題
-
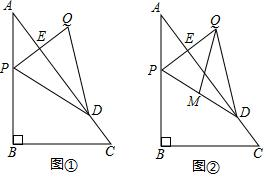1．如圖①，在△ABC中，∠ABC=90°，AB=4，BC=3．點P從點A出發，沿折線AB-BC以每秒5個單位長度的速度向點C運動，同時點D從點C出發，沿CA以每秒2個單位長度的速度向點A運動，點P到達點C時，點P、D同時停止運動．當點P不與點A、C重合時，作點P關于直線AC的對稱點Q，連接PQ交AC于點E，連接DP、DQ．設點P的運動時間為t秒，線段CE的長為y.
（1）求出y與t之間的函數關系式；
（2）當△PDQ為銳角三角形時，求t的取值范圍；
（3）如圖②，取PD的中點M，連接QM．當直線QM與△ABC的一條直角邊平行時，直接寫出t的值．發布：2025/5/26 8:0:5組卷：371引用：1難度：0.1 -
2．如圖，在△ABC和△DEF中，∠BAC=∠EDF=90°，AB=AC，DE=DF，BC、EF交于點M，且點M為BC、EF的中點，將△DEF繞點M旋轉．
（1）如圖1，當△DEF旋轉至點A在FD延長線上時，若BC=3，AF=2，tan∠BAF=6，求線段BF的長；5
（2）如圖2，當△DEF旋轉至點A在FD延長線上，點B在DE延長線上時，求證：BE+EF；2AF=2
（3）如圖3，在△DEF旋轉過程中，直線AD與直線CF交于點N，連接BN，P為BN的中點，連接AP，若AB=6，請直接寫出線段AP的最大值．2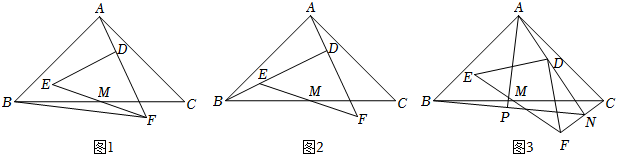
發布：2025/5/26 8:0:5組卷：256引用：1難度：0.3 -
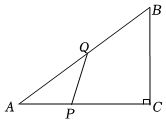3．如圖，在Rt△ABC中，∠C=90°，AC=8，BC=6．動點P從點A向點C運動，速度為10個單位/秒，作PQ=PA交射線AB于點Q，設點P的運動時間為t（秒）（0＜t＜4）．
（1）用含t的代數式表示線段AQ的長；
（2）當點Q與點B重合時，求PC的長；
（3）設△APQ和△ABC重合部分面積為S，當PC=BQ時，求S的值；
（4）設AC中點為D，連接DQ，設點P關于DQ的對稱點為P'，當P'落在AC邊上時，直接寫出t的值．發布：2025/5/26 7:0:2組卷：24引用：1難度：0.2