在平面直角坐標系中，已知點P₁（x₁，y₁），P₂（x₂，y₂），根據勾股定理，我們可以求得這兩個這點間的距離
P
1
P
2
=
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
．當點P₁P₂在坐標軸上或平行（垂直）于坐標軸的直線上時，兩點間的距離可簡化為P₁P₂=|x₁-x₂|，或P₁P₂=|y₁-y₂|．
請利用以上結論，回答下列問題：
（1）已知A（4，3），B（-2，-5），則A，B兩點間的距離為
10
10
；
（2）已知M，N在平行于x軸的直線上，點M的橫坐標為5，點N的橫坐標為-2，則M，N點兩之間的距離為
7
7
．
（3）已知一個三角形各頂點的坐標為D（-3，1），E（-2，-1），F（4，2），請判定此三角形的形狀，并說明理由．

【答案】10；7

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/7/6 8:0:9組卷：77引用：1難度：0.6

相似題

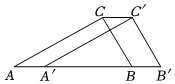1．如圖，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2cm.把△ABC沿AB方向平移1cm,得到△A'B'C'，連結CC'，則四邊形AB'C'C的周長為
cm.
發布：2025/5/21 17:0:2組卷：1152引用：7難度：0.5
解析
2．細心觀察如圖，認真分析各式，然后解答問題．
OA
2
2
=
1
+
（
1
）
2
，
S
1
=
1
2
，
OA
2
2
=
1
+
（
2
）
2
，
S
2
=
2
2
，
OA
2
4
=
1
+
（
3
）
2
，
S
3
=
3
2
，
?
（1）OA₁₀=
；
（2）用含n（n是正整數）的等式表示上述面積變化規律：
O
A
2
n
=
，S_n=
；
（3）若一個三角形的面積是
5
，則它是第
個三角形；
（4）求出
S
2
1
+
S
2
1
+
S
2
3
+
S
2
4
+
?
+
S
2
n
的值．
發布：2025/5/21 13:30:2組卷：131引用：1難度：0.4
解析
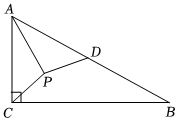3．如圖，在△ABC中，∠ACB=90°，AC=4，∠B=30°，點P在△ABC的內部，
PC
=
3
，D是AB的中點，連接PA，PD，當△PAD為等腰三角形時，PA的長為
．
發布：2025/5/21 16:30:2組卷：283引用：6難度：0.6
解析

相關試卷

1．如圖，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2cm.把△ABC沿AB方向平移1cm,得到△A'B'C'，連結CC'，則四邊形AB'C'C的周長為 cm.