閱讀并填空將三角尺（△MPN，∠MPN=90°）放置在△ABC上（點P在△ABC內），如圖1所示，三角尺的兩邊PM、PN恰好經過點B和點C．我們來探究：∠ABP與∠ACP是否存在某種數量關系．
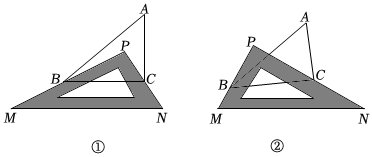
（1）特例探索：
若∠A=50°，則∠PBC+∠PCB=9090度；∠ABP+∠ACP=4040度；
（2）類比探索：
∠ABP、∠ACP、∠A的關系是 ∠ABP+∠ACP=90°-∠A∠ABP+∠ACP=90°-∠A；
（3）變式探索：
如圖2所示，改變三角尺的位置，使點P在△ABC外，三角尺的兩邊PM、PN仍恰好經過點B和點C，則∠ABP、∠ACP、∠A的關系是 ∠ACP-∠ABP=90°-∠A∠ACP-∠ABP=90°-∠A．
【考點】三角形內角和定理．
【答案】90；40；∠ABP+∠ACP=90°-∠A；∠ACP-∠ABP=90°-∠A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：181引用：6難度：0.8
相似題
-
1．已知BD、CE是△ABC的高，BD、CE所在的直線相交所成的角中有一個角為60°，則∠BAC=．
發布：2025/6/8 5:30:2組卷：764引用：4難度：0.6 -
2．如圖1，在△ABC中，∠B=90°，分別作其內角∠ACB與外角∠DAC的平分線，且兩條角平分線所在的直線交于點E．
（1）∠E=°；
（2）分別作∠EAB與∠ECB的平分線，且兩條角平分線交于點F．
①依題意在圖1中補全圖形；
②求∠AFC的度數；
（3）在（2）的條件下，射線FM在∠AFC的內部且∠AFM=∠AFC，設EC與AB的交點為H，射線HN在∠AHC的內部且∠AHN=13∠AHC，射線HN與FM交于點P，若∠FAH，∠FPH和∠FCH滿足的數量關系為∠FCH=m∠FAH+n∠FPH，請直接寫出m,n的值．13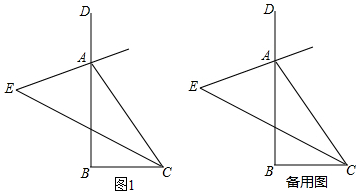
發布：2025/6/8 10:0:2組卷：3608引用：3難度：0.1 -
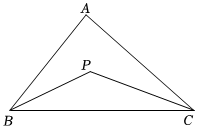3．如圖，在△ABC中，∠ABC=60°，∠ACB=40°，點P為∠ABC、∠ACB的角平分線上的交點．
（1）∠BPC的度數是 ．
（2）請問點P是否在∠BAC的角平分線上？請說明理由．發布：2025/6/8 5:0:1組卷：195引用：4難度：0.6