各頂點都在方格紙格點（橫豎格子線的交錯點）上的多邊形稱為格點多邊形．如何計算它的面積？奧地利數學家皮克（G?Pick,1859～1942年）證明了格點多邊形的面積公式S=a+12b-1，其中a表示多邊形內部的格點數，b表示多邊形邊界上的格點數，S表示多邊形的面積．如圖，a=4，b=6，S=4+12×6-1=6
（1）請在圖1中畫一個格點正方形，使它的內部只含有4個格點，并寫出它的面積．
（2）請在圖2中畫一個格點三角形，使它的面積為72，且每條邊上除頂點外無其它格點．
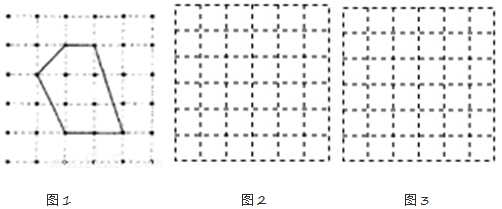
1
2
1
2
7
2
【考點】作圖—應用與設計作圖．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 14:0:0組卷：775引用：30難度：0.5
相似題
-
1．圖①，圖②，圖③都是4×4的正方形網格，每個小正方形的頂點稱為格點，每個小正方形的邊長均為1．在圖①，圖②中已畫出線段AB，在圖③中已畫出點A．按下列要求畫圖：
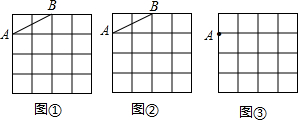
（1）在圖①中，以格點為頂點，AB為一邊畫一個等腰三角形；
（2）在圖②中，以格點為頂點，AB為一邊畫一個正方形；
（3）在圖③中，以點A為一個頂點，另外三個頂點也在格點上，畫一個面積最大的正方形．發布：2025/6/19 16:30:1組卷：692引用：33難度：0.7 -
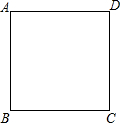2．如圖，在邊長為4的正方形ABCD中，請畫出以A為一個頂點，另外兩個頂點在正方形ABCD的邊上，且含邊長為3的所有大小不同的等腰三角形．（要求：只要畫出示意圖，并在所畫等腰三角形長為3的邊上標注數字3）發布：2025/6/19 16:30:1組卷：1991引用：43難度：0.5 -
3．已知△ABC的三條邊長分別為3，4，6，在△ABC所在平面內畫一條直線，將△ABC分割成兩個三角形，使其中的一個是等腰三角形，則這樣的直線最多可畫（ ）
發布：2025/6/19 16:0:1組卷：2710引用：47難度：0.5