閱讀下面材料：
實際問題：如圖（1），一圓柱的底面半徑為5厘米，BC是底面直徑，高AB為5厘米，求一只螞蟻從點A出發沿圓柱表面爬行到點C的最短路線，小明設計了兩條路線．

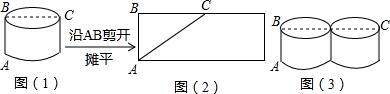
解決方案：
路線1：側面展開圖中的線段AC，如圖（2）所示，
設路線l的長度為l₁：則l₁²=AC²=AB²+BC²=5²+（5π）²=25+25π²；
路線2：高線AB+底面直徑BC，如圖（1）所示．
設路線2的長度為l₂：則l₂²=（AB+BC）²=（5+10）²=225．
為比較l₁，l₂的大小，我們采用“作差法”：
∵l₁²-l₂²=25（π²-8）＞0∴l₁²＞l₂²∴l₁＞l₂，
小明認為應選擇路線2較短．
（1）問題類比：
小亮對上述結論有些疑惑，于是他把條件改成：“圓柱的底面半徑為1厘米，高AB為5厘米．”．請你用上述方法幫小亮比較出l₁與l₂的大小：
（2）問題拓展：
請你幫他們繼續研究：在一般情況下，當圓柱的底面半徑為r厘米時，高為h厘米，螞蟻從A點出發沿圓柱表面爬行到點C，當

r

h

滿足什么條件時，選擇路線2最短？請說明理由．
（3）問題解決：
如圖（3）為2個相同的圓柱緊密排列在一起，高為5厘米，當螞蟻從點A出發沿圓柱表面爬行到C點的兩條路線長度相等時，求圓柱的底面半徑r.（注：按上面小明所設計的兩條路線方式）．