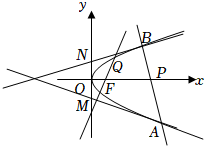
如圖，過拋物線E：y2=2px（p＞0）的焦點F的直線l1交拋物線于第一象限的點Q（2，y0），且QF=3，過點P（a,0）（a＞0）（不同于焦點F）的直線l2與拋物線E交于A，B，過A作拋物線的切線交y軸于M，過B作MP的平行線交y軸于N．
（Ⅰ）求拋物線方程及直線l1的斜率；
（Ⅱ）記S1為AM，BN與y軸圍成三角形的面積，是否存在實數λ使S△OAB=λS1，若存在，求出實數λ的值，若不存在，請說明理由．
【考點】拋物線的切線方程及性質．
【答案】（Ⅰ）y2=4x，2；（Ⅱ）存在λ=2，使S△OAB=λS1．
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：93引用：1難度：0.3
相似題
-
1．已知拋物線y=x2的焦點為F，過F且斜率為k的直線l交拋物線于A，B兩點，B在第一象限，過A，B分別作拋物線的切線l1，l2，且l1，l2相交于點P，若BP交x軸于點Q，則下列說法正確的有（ ）
發(fā)布：2024/7/18 8:0:9組卷：61引用：2難度：0.5 -
2．已知F為拋物線C：y2=4x的焦點，O為坐標原點，過F作兩條互相垂直的直線l1，l2，直線l1與C交于A，B兩點，直線l2與C交于D，E兩點，
（1）當A的縱坐標為4時，求拋物線C在點A處的切線方程；
（2）四邊形ADBE面積的最小值．發(fā)布：2024/7/19 8:0:9組卷：32引用：2難度：0.4 -
3．已知x2=2py（p＞0）的焦點為F，且經過F的直線被圓
截得的線段長度的最小值為4．（x-1）2+（y+32）2=9
（1）求拋物線的方程；
（2）設坐標原點為O，若過點（2，0）作直線l與拋物線相交于不同的兩點P，Q，過點P，Q作拋物線的切線分別與直線OQ，OP相交于點M，N，請問直線MN是否經過定點？若是，請求出此定點坐標，若不是，請說明理由．發(fā)布：2024/8/28 8:0:8組卷：73引用：2難度：0.2